题目内容
11.设函数$f(x)=|{\frac{1}{x}-1}|$(x>0).(1)写出函数f(x)的单调区间(不要求推理过程);
(2)是否存在正实数m,n(m<n),使函数f(x)的定义域为[m,n]时值域为$[\frac{m}{3},\frac{n}{3}]$?若存在,求m,n的值;若不存在,请说明理由.
分析 (1)根据函数单调性的性质进行求解即可.
(2)根据函数定义域和值域的关系建立方程组关系进行求解即可.
解答 解:(1)函数f(x)的单调递减区间是(0,1](或(0,1)),单调递增区间是(1,+∞)(或[1,+∞)) …(4分)
(2)∵$f(x)=\left\{\begin{array}{l}\frac{1}{x}-1\\ 1-\frac{1}{x}\end{array}\right.$,$\begin{array}{l}x∈(0,1]\\ \\ x∈(1,+∞)\end{array}$…(6分)
∴若存在符合题意的m,n,则
①当0<m<n≤1时,有$\left\{\begin{array}{l}f(m)=\frac{1}{m}-1=\frac{n}{3}\\ f(n)=\frac{1}{n}-1=\frac{m}{3}\end{array}\right.$,即$\left\{\begin{array}{l}3-3m=mn\\ 3-3n=mn\end{array}\right.$
解得m=n,这与m<n相矛盾 …(8分)
②当0<m<1<n时,由于$f(1)=0∈[\frac{m}{3},\frac{n}{3}]$
∴$\frac{m}{3}$≤0<$\frac{n}{3}$,即m≤0<n,这与m>0相矛盾 …(10分)
③当1≤m<n时,有$\left\{\begin{array}{l}f(m)=1-\frac{1}{m}=\frac{m}{3}\\ f(n)=1-\frac{1}{n}=\frac{n}{3}\end{array}\right.$,即$\left\{\begin{array}{l}{m^2}-3m+3=0\\{n^2}-3n+3=0\end{array}\right.$
∴m,n是方程x2-3x+3=0的两根
∵△=(-3)2-4×3=-3<0
∴x2-3x+3=0没有实根,即不存在满足题设的正实数m,n
…(13分)
综上所述可知不存在正实数m,n满足题设.…(14分)
点评 本题主要考查函数单调性的判断以及函数值域的求解和应用,建立方程关系是解决本题的关键.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案| P(K2>k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 有99.5%以上的把握认为“爱好该项运动与性别无关” | |
| B. | 有99.5%以上的把握认为“爱好该项运动与性别有关” | |
| C. | 在犯错误的概率不超过0.05%的前提下,认为“爱好该项运动与性别有关” | |
| D. | 在犯错误的概率不超过0.05%的前提下,认为“爱好该项运动与性别无关” |
| A. | 2y<2x | B. | logx4<logy4 | C. | log3x<log3y | D. | ${(\frac{1}{2})^x}<{(\frac{1}{2})^y}$ |
| A. | 2个 | B. | 1个 | C. | 0个 | D. | 无数个 |
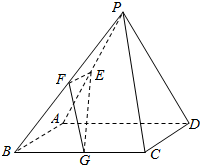 已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,且平面PAD⊥平面ABCD,E,F,G分别是PA、PB、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,且平面PAD⊥平面ABCD,E,F,G分别是PA、PB、BC的中点.