题目内容
12.关于函数f(x)=cos(2x-$\frac{π}{3}$)+cos(2x+$\frac{π}{6}$),则下列命题:①y=f(x)的最大值为$\sqrt{2}$;
②y=f(x)最小正周期是π;
③y=f(x)在区间($\frac{π}{24}$,$\frac{13π}{24}$)上是减函数;
④将函数y=$\sqrt{2}$cos2x的图象向右平移$\frac{π}{24}$个单位后,将与已知函数的图象重合.
其中正确命题的序号是①②③④.
分析 利用诱导公式以及辅助角公式基本公式将函数化为y=Asin(ωx+φ)的形式,结合三角函数的图象和性质,依次判断各选项即可.
解答 解:函数f(x)=cos(2x-$\frac{π}{3}$)+cos(2x+$\frac{π}{6}$)=sin(2x+$\frac{π}{6}$)+cos(2x+$\frac{π}{6}$)=$\sqrt{2}$sin(2x$+\frac{π}{6}+\frac{π}{4}$)=$\sqrt{2}$sin(2x+$\frac{5π}{12}$)
对于①:由三角函数的图象和性质,f(x)的最大值为$\sqrt{2}$;∴①对;
对于②:f(x)最小正周期T=$\frac{2π}{2}=π$,∴②对;
对于③:由$\frac{π}{2}+2kπ≤$2x+$\frac{5π}{12}$$≤\frac{3π}{2}+2kπ$,k∈Z,可得$\frac{π}{24}$+kπ≤x≤$\frac{13π}{24}$+kπ,∴f(x)在区间($\frac{π}{24}$,$\frac{13π}{24}$)上是减函数;∴③对;
对于④:将函数y=$\sqrt{2}$cos2x的图象向右平移$\frac{π}{24}$个单位后,可得$\sqrt{2}$cos2(x-$\frac{π}{24}$)=$\sqrt{2}$cos(2x-$\frac{π}{12}$)=$\sqrt{2}$sin(2x$-\frac{π}{12}$$+\frac{π}{2}$)=$\sqrt{2}$sin(2x+$\frac{5π}{12}$),∴④对.
故答案为:①②③④.
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,利用三角函数公式将函数进行化简是解决本题的关键.属于中档题.

| A. | $\frac{{\sqrt{6}}}{4}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{10}}}{4}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
| 使用年数x(单位:米) | 2 | 3 | 4 | 5 | 6 |
| 维修总费用y(单位:万元) | 1.5 | 4.5 | 5.5 | 6.5 | 7.5 |
| X | 0 | 1 |
| P | 10a2-a | 2-6a |
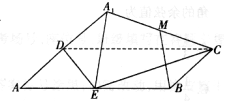 如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中:
如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中: