题目内容
17.某设备的使用年数x与所支出的维修总费用y的统计数据如下表:| 使用年数x(单位:米) | 2 | 3 | 4 | 5 | 6 |
| 维修总费用y(单位:万元) | 1.5 | 4.5 | 5.5 | 6.5 | 7.5 |
分析 根据表中数据计算$\overline{x}$、$\overline{y}$,代入回归直线方程$\widehat{y}$=1.3x+$\widehat{a}$求出$\widehat{a}$,再由回归直线方程求出$\widehat{y}$≥12时x的值即可.
解答 解:根据表中数据,计算$\overline{x}$=$\frac{1}{5}$×(2+3+4+5+6)=4,
$\overline{y}$=$\frac{1}{5}$×(1.5+4.5+5.5+6.5+7.5)=5.1,
且回归直线方程$\widehat{y}$=1.3x+$\widehat{a}$过样本中心点($\overline{x}$,$\overline{y}$),
∴5.1=1.3×4+$\widehat{a}$,
解得$\widehat{a}$=-0.1;
∴回归直线方程为$\widehat{y}$=1.3x-0.1;
令$\widehat{y}$=1.3x-0.1≥12,
解得x≥9.308,
据此模型预测该设备最多可使用10年,其维修总费用超过12万元,就应报废.
故答案为:10.
点评 本题考查了回归直线方程过样本中心点($\overline{x}$,$\overline{y}$)的应用问题,是基础题.

练习册系列答案
相关题目
7.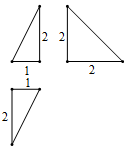 已知某三棱锥的三视图如图所示,图中的3个直角三角形的直角边长度已经标出,则在该三棱锥中,最短的棱和最长的棱所在直线的成角余弦值为( )
已知某三棱锥的三视图如图所示,图中的3个直角三角形的直角边长度已经标出,则在该三棱锥中,最短的棱和最长的棱所在直线的成角余弦值为( )
 已知某三棱锥的三视图如图所示,图中的3个直角三角形的直角边长度已经标出,则在该三棱锥中,最短的棱和最长的棱所在直线的成角余弦值为( )
已知某三棱锥的三视图如图所示,图中的3个直角三角形的直角边长度已经标出,则在该三棱锥中,最短的棱和最长的棱所在直线的成角余弦值为( )| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
5. 把一个皮球放入如图所示的由8根长均为20cm的铁丝接成的四棱锥形骨架内,使皮球的表面与8根铁丝都相切,则皮球的半径为( )
把一个皮球放入如图所示的由8根长均为20cm的铁丝接成的四棱锥形骨架内,使皮球的表面与8根铁丝都相切,则皮球的半径为( )
 把一个皮球放入如图所示的由8根长均为20cm的铁丝接成的四棱锥形骨架内,使皮球的表面与8根铁丝都相切,则皮球的半径为( )
把一个皮球放入如图所示的由8根长均为20cm的铁丝接成的四棱锥形骨架内,使皮球的表面与8根铁丝都相切,则皮球的半径为( )| A. | l0$\sqrt{3}$cm | B. | 10 cm | C. | 10$\sqrt{2}$cm | D. | 30cm |
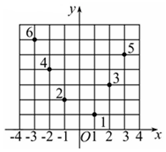 如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列{an}(n∈N*)的前12项(即横坐标为奇数项,纵坐标为偶数项),按如此规律下去,则a2009+a2010+a2011等于( )
如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列{an}(n∈N*)的前12项(即横坐标为奇数项,纵坐标为偶数项),按如此规律下去,则a2009+a2010+a2011等于( )