题目内容
2.化简求值:($\frac{x-1}{{x}^{2}-1}$+$\frac{1}{x+1}$)÷$\frac{4}{{x}^{2}+x}$,其中x=-2.分析 利用乘法公式、约分化简代入即可得出.
解答 解:($\frac{x-1}{{x}^{2}-1}$+$\frac{1}{x+1}$)÷$\frac{4}{{x}^{2}+x}$=$\frac{2}{x+1}$×$\frac{x(x+1)}{4}$=$\frac{x}{2}$,
当x=-2时.
原式=$\frac{-2}{2}$=-1.
点评 本题考查了乘法公式、约分化简方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
10.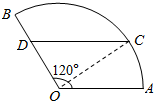 如图,某住宅小区的平面图呈圆心角为120°的扇形AOB,C是该小区的一个出入口,且小区里有一条平行于AO的小路CD.已知某人从O沿OD走到D用了2分钟,从D沿着DC走到C用了3分钟.若此人步行的速度为每分钟50米,则该扇形的半径的长度为( )
如图,某住宅小区的平面图呈圆心角为120°的扇形AOB,C是该小区的一个出入口,且小区里有一条平行于AO的小路CD.已知某人从O沿OD走到D用了2分钟,从D沿着DC走到C用了3分钟.若此人步行的速度为每分钟50米,则该扇形的半径的长度为( )
 如图,某住宅小区的平面图呈圆心角为120°的扇形AOB,C是该小区的一个出入口,且小区里有一条平行于AO的小路CD.已知某人从O沿OD走到D用了2分钟,从D沿着DC走到C用了3分钟.若此人步行的速度为每分钟50米,则该扇形的半径的长度为( )
如图,某住宅小区的平面图呈圆心角为120°的扇形AOB,C是该小区的一个出入口,且小区里有一条平行于AO的小路CD.已知某人从O沿OD走到D用了2分钟,从D沿着DC走到C用了3分钟.若此人步行的速度为每分钟50米,则该扇形的半径的长度为( )| A. | $50\sqrt{5}$ | B. | $50\sqrt{7}$ | C. | $50\sqrt{11}$ | D. | $50\sqrt{19}$ |