题目内容
17.函数y=$\sqrt{1-2cosx}$的减区间为[-π+2kπ,-$\frac{π}{3}$+2kπ](k∈Z).分析 先求出函数的定义域,利用余弦函数y=cosx的单调性和y=${x}^{\frac{1}{2}}$,即可判定y=$\sqrt{1-2cosx}$的减区间.
解答 解:由y=$\sqrt{1-2cosx}$得1-2cosx≥0,即cosx≤$\frac{1}{2}$,即-π+2kπ≤x≤-$\frac{π}{3}$+2kπ,或$\frac{π}{3}$+2kπ≤x≤2kπ+π,k∈Z,
设t=1-2cosx,
∵余弦函数y=cosx在[-π+2kπ,2kπ-$\frac{π}{3}$](k∈Z)上是增函数,在[2kπ+$\frac{π}{3}$,π+2kπ](k∈Z)上是减函数,
且函数t=1-2cosx的单调性与余弦函数的单调性相反,
∴函数t=1-2cosx在[-π+2kπ,2kπ-$\frac{π}{3}$],(k∈Z)上是减函数,
∵y=${x}^{\frac{1}{2}}$在[0,+∞)为增函数,
∴y=$\sqrt{1-2cosx}$的减区间为[-π+2kπ,-$\frac{π}{3}$+2kπ](k∈Z).
故答案为:[-π+2kπ,-$\frac{π}{3}$+2kπ](k∈Z).
点评 本题考查了复合函数的单调性应用,以及余弦函数的单调性问题,关键是求出函数的定义域,属于基础题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
8.在△ABC中,∠C=60°,AC=2,BC=3,那么AB等于( )
| A. | $\sqrt{5}$ | B. | $\sqrt{6}$ | C. | $\sqrt{7}$ | D. | $2\sqrt{2}$ |
5.下列函数为奇函数的是( )
| A. | y=x3+3x2 | B. | y=$\frac{{e}^{x}+{e}^{-x}}{2}$ | C. | y=xsinx | D. | y=log2$\frac{3-x}{3+x}$ |
2.某医院对治疗支气管肺炎的两种方案A,B进行比较研究,将志愿者分为两组,分别采用方案A和方案B进行治疗,统计结果如下:
(1)完成上述列联表,并比较两种治疗方案有效的频率;
(2)能否在犯错误的概率不超过0.05的前提下认为治疗是否有效与方案选择有关?
| 有效 | 无效 | 合计 | |
| 使用方案A组 | 96 | 120 | |
| 使用方案B组 | 72 | ||
| 合计 | 32 |
(2)能否在犯错误的概率不超过0.05的前提下认为治疗是否有效与方案选择有关?
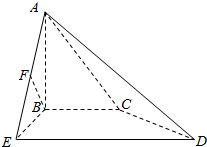 如图,四棱锥A-BCDE中,AB、BC、BE两两垂直且AB=BC=BE,DE∥BC,DE=2BC,F是AE的中点.
如图,四棱锥A-BCDE中,AB、BC、BE两两垂直且AB=BC=BE,DE∥BC,DE=2BC,F是AE的中点.