题目内容
5．由直线x+y+2=0，x+2y+1=0，2x+y+1=0围成的三角形区域（包括边界）用不等式（组）可表示为$\left\{\begin{array}{l}{x+y+2≥0}\\{x+2y+1≤0}\\{2x+y+1≤0}\end{array}\right.$．分析 作出直线，确定平面区域与直线的位置关系即可得到结论．
解答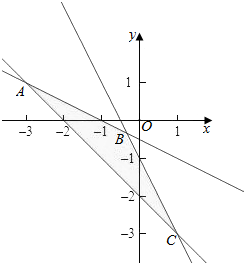 
解：作出三条直线，则对应的区域为△ABC，
由图象知，区域在线x+y+2=0的上方，x+2y+1=0的下方，2x+y+1=0的下方，
则对应的不等式组为$\left\{\begin{array}{l}{x+y+2≥0}\\{x+2y+1≤0}\\{2x+y+1≤0}\end{array}\right.$，
故答案为：$\left\{\begin{array}{l}{x+y+2≥0}\\{x+2y+1≤0}\\{2x+y+1≤0}\end{array}\right.$．
点评 本题主要考查二元一次不等式组表示平面区域，利用区域与不等式的关系是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
