题目内容
已知∠BAC在平面α内,PA是α的斜线,若∠PAB=∠PAC=∠BAC=60°,PA=a,则点P到平面α的距离为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:作PO⊥α,垂足为O,作OD⊥AB,垂足为D,连接PD,则PD⊥AB,求出OA,可得PO.
解答:
解:作PO⊥α,垂足为O,作OD⊥AB,垂足为D,连接PD,则PD⊥AB,
∵∠PAB=∠PAC=∠BAC=60°,
∴AD=
a,∠OAB=30°,
∴OA=
a,
∴PO=
=
a.
故选:C.

∵∠PAB=∠PAC=∠BAC=60°,
∴AD=
| 1 |
| 2 |
∴OA=
| ||
| 3 |
∴PO=
a2-
|
| ||
| 3 |
故选:C.
点评:本题考查点到平面的距离的求法,是中档题,解题时要认真审题,注意构造法的合理运用.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
已知a>0,b>0,若不等式mab≤(3a+b)(b+3a)恒成立,则m的最大值等于( )
| A、12 | B、9 | C、6 | D、3 |
已知函数f(x)=cos
,根据下列框图,输出S的值为( )

| πx |
| 3 |

| A、670 | ||
B、670
| ||
| C、671 | ||
| D、672 |
在△ABC中,角A,B,C的对边分别a,b,c,若a2+b2=
c2.则直线ax-by+c=0被圆x2+y2=9所截得的弦长为( )
| 1 |
| 2 |
A、2
| ||
B、3
| ||
C、2
| ||
D、3
|
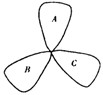 荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图.假设现在青蛙在A叶上,则跳三次之后停在A叶上的概率是( )
荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图.假设现在青蛙在A叶上,则跳三次之后停在A叶上的概率是( )