Question

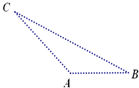如图，某林场为了及时发现火情，在林场中设立了两个观测点A和B，某日两个观测点的林场人员分别观测到C处有险情．在A处观测到火情发生在北偏西45°方向，在B点观测火场C在北偏西75°方向，已知B在A的正东方向10km处，那么火场C到观测点A的距离为

 

km．

Answer 1

考点：余弦定理,正弦定理

专题：三角函数的求值

分析：根据题意求出∠ABC的度数，在三角形ABC中，利用正弦定理即可求出AC的长．

解答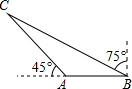： 解：如图所示，∠ABC=15°，∠C=30°，
在△ABC中，AB=10km，sin15°=sin（45°-30°）=sin45°cos30°-cos45°sin30°=

2

2

×

3

2

-

2

2

×

1

2

=

6 - 2

4

，
由正弦定理得：

AC

sin∠ABC

=

AB

sinC

，
∴AC=

ABsin∠ABC

sinC

=

10×sin15°

sin30°

=

10× 6 - 2 4

1 2

=5（

6

-

2

）km，
则火场C到观测点A的距离为5（

6

-

2

）km．
故答案为：5（

6

-

2

）

点评：此题考查了正弦定理，以及特殊角的三角函数值，熟练掌握正弦定理是解本题的关键．