题目内容
(坐标系与参数方程)已知曲线C的极坐标方程ρ=-2sinθ,直线l的参数方程是
(t为参数),则曲线C上的点到直线l的最短距离是 .
|
考点:直线的参数方程,简单曲线的极坐标方程
专题:计算题,坐标系和参数方程
分析:由题意将曲线C和直线l先化为一般方程坐标,然后再计算曲线C上的点到直线l的最短距离.
解答:
解:曲线C的极坐标方程ρ=-2sinθ,直角坐标方程为:x2+y2=-2y,即x2+(y+1)2=1.
直线l的参数方程是
(t为参数),普通方程为4x+3y-8=0.
∵圆心(0,-1)到直线的距离为
=
,
∴曲线C上的点到直线l的最短距离是
-1=
,
故答案为:
直线l的参数方程是
|
∵圆心(0,-1)到直线的距离为
| |-3-8| |
| 5 |
| 11 |
| 5 |
∴曲线C上的点到直线l的最短距离是
| 11 |
| 5 |
| 6 |
| 5 |
故答案为:
| 6 |
| 5 |
点评:此题考查参数方程与普通方程的区别和联系,两者要会互相转化,根据实际情况选择不同的方程进行求解,这也是每年高考必考的热点问题.

练习册系列答案
相关题目
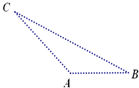 如图,某林场为了及时发现火情,在林场中设立了两个观测点A和B,某日两个观测点的林场人员分别观测到C处有险情.在A处观测到火情发生在北偏西45°方向,在B点观测火场C在北偏西75°方向,已知B在A的正东方向10km处,那么火场C到观测点A的距离为
如图,某林场为了及时发现火情,在林场中设立了两个观测点A和B,某日两个观测点的林场人员分别观测到C处有险情.在A处观测到火情发生在北偏西45°方向,在B点观测火场C在北偏西75°方向,已知B在A的正东方向10km处,那么火场C到观测点A的距离为