题目内容
在平面直角坐标系xOy中,若圆C的圆心在第一象限,圆C与x轴相交于A(1,0)、B(3,0)两点,且与直线x-y+1=0相切,则圆C的标准方程为 .
考点:圆的标准方程
专题:直线与圆
分析:由已知条件设圆心坐标为(2,b)(b>0),由圆与直线x-y+1=0相切,求出圆C的圆心和半径r.由此能求出圆C的标准方程.
解答:
解:∵圆C的圆心在第一象限,圆C与x轴相交于A(1,0)、B(3,0)两点,
∴设圆心坐标为(2,b)(b>0),
∵圆与直线x-y+1=0相切,
∴
=
,
∴b2+6b-7=0,解得b=1或b=-7,
∵b>0,∴b=1
∴圆C的圆心C(2,1),半径r=
=
.
∴圆C的标准方程为(x-2)2+(y-1)2=2
故答案为:(x-2)2+(y-1)2=2.
∴设圆心坐标为(2,b)(b>0),
∵圆与直线x-y+1=0相切,
∴
| (2-1)2+b2 |
| |2-b+1| | ||
|
∴b2+6b-7=0,解得b=1或b=-7,
∵b>0,∴b=1
∴圆C的圆心C(2,1),半径r=
| (2-1)2+12 |
| 2 |
∴圆C的标准方程为(x-2)2+(y-1)2=2
故答案为:(x-2)2+(y-1)2=2.
点评:本题考查圆的标准方程的求法,是中档题,解题时要认真审题,注意点到直线的距离公式的合理运用.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
不等式x2<|x-1|+a的解集是区间(-3,3)的子集,则实数a的取值范围是( )
| A、(-∞,5] |
| B、(-∞,5) |
| C、(-∞,7] |
| D、(-∞,7) |
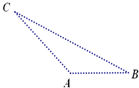 如图,某林场为了及时发现火情,在林场中设立了两个观测点A和B,某日两个观测点的林场人员分别观测到C处有险情.在A处观测到火情发生在北偏西45°方向,在B点观测火场C在北偏西75°方向,已知B在A的正东方向10km处,那么火场C到观测点A的距离为
如图,某林场为了及时发现火情,在林场中设立了两个观测点A和B,某日两个观测点的林场人员分别观测到C处有险情.在A处观测到火情发生在北偏西45°方向,在B点观测火场C在北偏西75°方向,已知B在A的正东方向10km处,那么火场C到观测点A的距离为