Question

16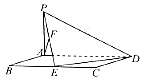．如图，平行四边形ABCD中，BC=2AB=4，∠ABC=60°，PA⊥平面ABCD，PA=2，E，F分别为BC，PE的中点．
（1）求证：AF⊥平面PED；
（2）求点C到平面PED的距离．

Answer 1

分析 （1）连接AE，推导出AE⊥ED，PA⊥ED，从而ED⊥平面PAE，进而ED⊥AF，再求出AF⊥PE，由此能证明AF⊥平面PED．
（2）设点C到平面PED的距离为d，由V_C-PED=V_P-ECD，能求出点C到平面PED的距离．

解答 证明：（1）连接AE，在平行四边形ABCD中，
BC=2AB=4，∠ABC=60°，
∴AE=2，$ED=2\sqrt{3}$，从而有AE²+ED²=AD²，
∴AE⊥ED．
∵PA⊥平面ABCD，ED?平面ABCD，∴PA⊥ED，
又∵PA∩AE=A，∴ED⊥平面PAE，AF?平面PAE
从而有ED⊥AF．
又∵PA=AE=2，F为PE的中点，
∴AF⊥PE，又∵PE∩ED=E，
∴AF⊥平面PED．
解：（2）设点C到平面PED的距离为d，
在Rt△PED中，$PE=2\sqrt{2}$，$ED=2\sqrt{3}$，∴${S_{△PED}}=2\sqrt{6}$．
在△ECD中，EC=CD=2，∠ECD=120°，∴${S_{△ECD}}=\sqrt{3}$．
由V_C-PED=V_P-ECD得，$\frac{1}{3}{S_{△PED}}•d=\frac{1}{3}{S_{△ECD}}•PA$，
∴$d=\frac{{{S_{△ECD}}•PA}}{{{S_{△PED}}}}=\frac{{\sqrt{2}}}{2}$．
所以点C到平面PED的距离为$\frac{{\sqrt{2}}}{2}$．

点评 本题考查线面垂直的证明，考查点到平面的距离的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查推理论证能力、运算求解能力、空间想象能力，考查化归与转化思想、数形结合思想，是中档题．