题目内容
19.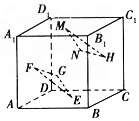 如图,在正方体ABCD-A1B1C1D1中中,E,F,G,H,M,N分别是正方体六个面的中心,求证:平面EFG∥平面HMN.
如图,在正方体ABCD-A1B1C1D1中中,E,F,G,H,M,N分别是正方体六个面的中心,求证:平面EFG∥平面HMN.
分析 以点D为坐标原点,分别以DA,DC,DD1所在的直线为x轴,y轴,z轴建立空间直角坐标系Dxyz,得到$\overrightarrow{EF}$∥$\overrightarrow{HM}$,$\overrightarrow{FG}$∥$\overrightarrow{NH}$,从而证出结论.
解答 证明:以点D为坐标原点,分别以DA,DC,DD1所在的直线为x轴,y轴,z轴建立空间直角坐标系Dxyz,
如图示:
不妨设正方体的棱长为2,
则E(1,1,0),F(1,0,1),G(2,1,1),
H(1,2,1),M(1,1,2),N(0,1,1).
所以$\overrightarrow{EF}$=(0,-1,1),
$\overrightarrow{FG}$=(1,1,0),
$\overrightarrow{HM}$=(0,-1,1),
$\overrightarrow{NH}$=(1,1,0),
所以$\overrightarrow{EF}$∥$\overrightarrow{HM}$,$\overrightarrow{FG}$∥$\overrightarrow{NH}$
∴EF∥HM,FG∥NH.
因为HM⊆平面HMN,NH⊆平面HMN,
所以EF∥平面HMN,FG∥平面HMN.
因为EF⊆平面EFG,FG⊆平面EFG,
EF∩FG=F,
所以平面EFG∥平面HMN.
点评 本题考查了面面平行问题,考查向量的应用,是一道中档题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
10.已知圆M过三点A(0,0),B(1,1),C(4,2),过点D(-1,4)作圆M的两条切线,两切点分别为E,F,
(I) 求圆M的方程.
(II) 求切线DE,DF方程
( III)求直线EF的方程.
(I) 求圆M的方程.
(II) 求切线DE,DF方程
( III)求直线EF的方程.
14.已知函数f(x)=$\left\{\begin{array}{l}{kx-1,x≤0}\\{{2}^{-x}-1,x>0}\end{array}\right.$,(k<0),当方程f[f(x)]=-$\frac{1}{2}$恰有三个实数根时,实数k的取值范围为( )
| A. | (-$\frac{1}{2}$,0) | B. | [-$\frac{1}{2}$,0) | C. | (-∞,-$\frac{1}{2}$] | D. | (-∞,-$\frac{1}{2}$) |