题目内容
10.已知圆M过三点A(0,0),B(1,1),C(4,2),过点D(-1,4)作圆M的两条切线,两切点分别为E,F,(I) 求圆M的方程.
(II) 求切线DE,DF方程
( III)求直线EF的方程.
分析 (I)设圆M的方程为x2+y2+Dx+Ey+F=0,代入坐标,可得方程组,即可求圆M的方程.
(II)分类讨论,利用圆心到直线的距离等于半径,即可求切线DE,DF方程
(III)求出点E,F在以DM为直径的圆,即可求直线EF的方程.
解答 解:(I) 设圆M的方程为x2+y2+Dx+Ey+F=0
则 $\left\{\begin{array}{l}F=0\\ 2+D+E+F=0\\ 20+4D+2E+F=0\end{array}\right.$…(2分)
解得D=-8,E=6,F=0所以圆M的方程是x2+y2-8x+6y=0…(4分)
(II) 圆M的方程是(x-4)2+(y+3)2=25
当切线的斜率不存在时,直线x=-1满足题意 …(5分)
当切线的斜率存在时,设切线方程为y-4=k(x+1),kx-y+k+4=0
由相切可知$\frac{{|{5k+7}|}}{{\sqrt{{k^2}+1}}}=5$解得$k=-\frac{12}{35}$,该切线方程为12x+35y-128=0
所以切线DE,DF方程为x=-1和 12x+35y-128=0…(8分)
(III)点E,F在以DM为直径的圆上,该圆方程为(x+1)(x-4)+(y-4)(y+3)=0
化简得x2+y2-3x-y-16=0,…(10分)
线段EF是两圆公共弦x2+y2-3x-y-16=0…①x2+y2-8x+6y=0…②
①-②得5x-7y-16=0,所以直线EF的方程为5x-7y-16=0…(12分)
点评 本题考查直线与圆的方程,考查圆与圆的位置关系,属于中档题.

练习册系列答案
相关题目
20.已知全集U={1,2,3,4,5,6,7,8},集合A={2,3,5,6},集合B={1,3,4,6,7},则集合A∩(∁UB)等于( )
| A. | {2,5} | B. | {3,6} | C. | {2,5,6} | D. | {2,3,5,6,8} |
1.在圆x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足,线段PD中点为M,当点P在圆上运动时,点M到直线l:x-y+1=0距离最大值为( )
| A. | $\frac{{\sqrt{10}+\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{10}-\sqrt{2}}}{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
18.某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)在某一周期内的图象时,列表并填入部分数据,如表:
(1)请将上表数据补充完整,填写在答题卡相应的位置,并求f(x)的解析式;
(2)将函数f(x)的图象上每一点的纵坐标缩短到原来的$\frac{1}{2}$倍,横坐标不变,得到函数g(x)的图象.试求g(x)在区间[π,$\frac{5π}{2}$]上的最值.
(1)请将上表数据补充完整,填写在答题卡相应的位置,并求f(x)的解析式;
(2)将函数f(x)的图象上每一点的纵坐标缩短到原来的$\frac{1}{2}$倍,横坐标不变,得到函数g(x)的图象.试求g(x)在区间[π,$\frac{5π}{2}$]上的最值.
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | 2π | $\frac{13π}{2}$ | |||
| f(x) | 0 | 4 | -4 | 0 |
15. 函数y=Asin($\overline{ω}$x+φ)(A>0,$\overline{ω}$>0,0<φ<π)在一个周期内的图象如图,此函数的解析式为( )
函数y=Asin($\overline{ω}$x+φ)(A>0,$\overline{ω}$>0,0<φ<π)在一个周期内的图象如图,此函数的解析式为( )
 函数y=Asin($\overline{ω}$x+φ)(A>0,$\overline{ω}$>0,0<φ<π)在一个周期内的图象如图,此函数的解析式为( )
函数y=Asin($\overline{ω}$x+φ)(A>0,$\overline{ω}$>0,0<φ<π)在一个周期内的图象如图,此函数的解析式为( )| A. | y=2sin(2x+$\frac{2π}{3}$) | B. | y=2sin(2x+$\frac{π}{3}$) | C. | y=2sin($\frac{x}{2}$-$\frac{π}{3}$) | D. | y=2sin(2x-$\frac{π}{3}$) |
2.已知全集U=R,A={x|-2≤x≤4},B={x|-3≤x≤3},求(∁UA)∩(∁UB)=( )
| A. | {x|-2≤x≤3} | B. | {x|x<-2或x>4} | C. | {x|-3≤x≤4} | D. | {x|x<-3或x>4} |
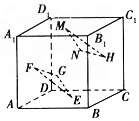 如图,在正方体ABCD-A1B1C1D1中中,E,F,G,H,M,N分别是正方体六个面的中心,求证:平面EFG∥平面HMN.
如图,在正方体ABCD-A1B1C1D1中中,E,F,G,H,M,N分别是正方体六个面的中心,求证:平面EFG∥平面HMN.