题目内容
7.已知函数f(x)=x+$\frac{a}{x}$+3,x∈N*,在x=5时取到最小值,则实数a的所有取值的集合为[20,30].分析 先求导,判断函数的单调性得到函数的最小值,由题意可得x取离$\sqrt{a}$最近的正整数使f(x)达到最小,得到,f(5)≤f(6),f(4)≥f(5),解得即可.
解答 解:∵f(x)=x+$\frac{a}{x}$+3,x∈N*,
∴f′(x)=1-$\frac{a}{{x}^{2}}$=$\frac{{x}^{2}-a}{{x}^{2}}$,
当a≤0时,f′(x)≥0,函数f(x)为增函数,最小值为f(x)min=f(1)=4+a,不满足题意,
当a>0时,令f′(x)=0,解得x=$\sqrt{a}$,
当0<x<$\sqrt{a}$时,即f′(x)<0,函数单调递减,
当x>$\sqrt{a}$时,即f′(x)>0,函数单调递增,
∴当x=$\sqrt{a}$时取最小值,
∵x∈N*,
∴x取离$\sqrt{a}$最近的正整数使f(x)达到最小,
∵x=5时取到最小值,
∴5<$\sqrt{a}$<6,或4<$\sqrt{a}$≤5
∴f(5)≤f(6)且f(4)≥f(5),
∴4+$\frac{a}{4}$+3≥5+$\frac{a}{5}$+3且5+$\frac{a}{5}$+3≤6+$\frac{a}{6}$+3
解得20≤a≤30
故答案为:[20,30]
点评 本题考查了导数和函数的单调性关系,以及参数的取值范围,属于中档题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)在某一周期内的图象时,列表并填入部分数据,如表:
(1)请将上表数据补充完整,填写在答题卡相应的位置,并求f(x)的解析式;
(2)将函数f(x)的图象上每一点的纵坐标缩短到原来的$\frac{1}{2}$倍,横坐标不变,得到函数g(x)的图象.试求g(x)在区间[π,$\frac{5π}{2}$]上的最值.
(1)请将上表数据补充完整,填写在答题卡相应的位置,并求f(x)的解析式;
(2)将函数f(x)的图象上每一点的纵坐标缩短到原来的$\frac{1}{2}$倍,横坐标不变,得到函数g(x)的图象.试求g(x)在区间[π,$\frac{5π}{2}$]上的最值.
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | 2π | $\frac{13π}{2}$ | |||
| f(x) | 0 | 4 | -4 | 0 |
15. 函数y=Asin($\overline{ω}$x+φ)(A>0,$\overline{ω}$>0,0<φ<π)在一个周期内的图象如图,此函数的解析式为( )
函数y=Asin($\overline{ω}$x+φ)(A>0,$\overline{ω}$>0,0<φ<π)在一个周期内的图象如图,此函数的解析式为( )
 函数y=Asin($\overline{ω}$x+φ)(A>0,$\overline{ω}$>0,0<φ<π)在一个周期内的图象如图,此函数的解析式为( )
函数y=Asin($\overline{ω}$x+φ)(A>0,$\overline{ω}$>0,0<φ<π)在一个周期内的图象如图,此函数的解析式为( )| A. | y=2sin(2x+$\frac{2π}{3}$) | B. | y=2sin(2x+$\frac{π}{3}$) | C. | y=2sin($\frac{x}{2}$-$\frac{π}{3}$) | D. | y=2sin(2x-$\frac{π}{3}$) |
2.已知全集U=R,A={x|-2≤x≤4},B={x|-3≤x≤3},求(∁UA)∩(∁UB)=( )
| A. | {x|-2≤x≤3} | B. | {x|x<-2或x>4} | C. | {x|-3≤x≤4} | D. | {x|x<-3或x>4} |
 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ABC=90°,AB=$\sqrt{3}$,BC=1,AA1=3,BD⊥AC,M为线段CC1上一点.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ABC=90°,AB=$\sqrt{3}$,BC=1,AA1=3,BD⊥AC,M为线段CC1上一点.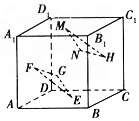 如图,在正方体ABCD-A1B1C1D1中中,E,F,G,H,M,N分别是正方体六个面的中心,求证:平面EFG∥平面HMN.
如图,在正方体ABCD-A1B1C1D1中中,E,F,G,H,M,N分别是正方体六个面的中心,求证:平面EFG∥平面HMN.