题目内容
9.对于函数f(x),若在定义域内存在实数x,满足f(-x)=-f(x),则称f(x)为“局部奇函数”,若f(x)=4x-m2x+1+m2-5为定义域R上的“局部奇函数”,则实数m的取值范围是1-$\sqrt{5}$<m≤2$\sqrt{3}$.分析 f(x)=4x-m2x+1+m2-5是定义在r上的“局部奇函数”,列出方程,可求出实数m的取值范围.
解答 解:f(x)=4x-m•2x+1+m2-5,f(-x)+f(x)=0可化为
4x+4-x-2m(2x+2-x)+2m2-10=0
令t=2x+2-x,则t∈[2,+∞),4x+4-x=t2-2,
即 t2-2mt+2m2-12=0在[2,+∞)有解,
即可保证f(x)为“局部中心对称函数”
令g(t)=t2-2mt+2m2-12
①当g(2)≤0时,t2-2mt+2m2-12=0在[2,+∞)有解,
由g(2)≤0,即2m2-4m-8≤0,解得1-$\sqrt{5}$≤m≤1+$\sqrt{5}$;
②当g(2)>0时,t2-2mt+2m2-12=0在[2,+∞)有解等价于
$\left\{\begin{array}{l}{△=4{m}^{2}-4(2{m}^{2}-12)≥0}\\{g(2)>0,m>2}\end{array}\right.$ 解得2<m≤2$\sqrt{3}$,
综上,所求实数m的取值范围为1-$\sqrt{5}$<m≤2$\sqrt{3}$.
故答案为:1-$\sqrt{5}$<m≤2$\sqrt{3}$.
点评 本题考查的知识点是函数奇偶性的性质,其中正确理解“局部奇函数”的概念是解答的关键.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
20.已知全集U={1,2,3,4,5,6,7,8},集合A={2,3,5,6},集合B={1,3,4,6,7},则集合A∩(∁UB)等于( )
| A. | {2,5} | B. | {3,6} | C. | {2,5,6} | D. | {2,3,5,6,8} |
1.在圆x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足,线段PD中点为M,当点P在圆上运动时,点M到直线l:x-y+1=0距离最大值为( )
| A. | $\frac{{\sqrt{10}+\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{10}-\sqrt{2}}}{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
18.某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)在某一周期内的图象时,列表并填入部分数据,如表:
(1)请将上表数据补充完整,填写在答题卡相应的位置,并求f(x)的解析式;
(2)将函数f(x)的图象上每一点的纵坐标缩短到原来的$\frac{1}{2}$倍,横坐标不变,得到函数g(x)的图象.试求g(x)在区间[π,$\frac{5π}{2}$]上的最值.
(1)请将上表数据补充完整,填写在答题卡相应的位置,并求f(x)的解析式;
(2)将函数f(x)的图象上每一点的纵坐标缩短到原来的$\frac{1}{2}$倍,横坐标不变,得到函数g(x)的图象.试求g(x)在区间[π,$\frac{5π}{2}$]上的最值.
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | 2π | $\frac{13π}{2}$ | |||
| f(x) | 0 | 4 | -4 | 0 |
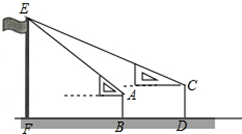 某校高一年级某班开展数学活动,小李和小军合作用一副三角板测量学校的旗杆,小李站在B点测得旗杆顶端E点的仰角为45°,小军站在点D测得旗杆顶端E点的仰角为30°,已知小李和小军相距(BD)6米,小李的身高(AB)1.5米,小军的身高(CD)1.75米,求旗杆的高EF的长.(结果精确到0.1,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
某校高一年级某班开展数学活动,小李和小军合作用一副三角板测量学校的旗杆,小李站在B点测得旗杆顶端E点的仰角为45°,小军站在点D测得旗杆顶端E点的仰角为30°,已知小李和小军相距(BD)6米,小李的身高(AB)1.5米,小军的身高(CD)1.75米,求旗杆的高EF的长.(结果精确到0.1,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73) 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ABC=90°,AB=$\sqrt{3}$,BC=1,AA1=3,BD⊥AC,M为线段CC1上一点.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ABC=90°,AB=$\sqrt{3}$,BC=1,AA1=3,BD⊥AC,M为线段CC1上一点.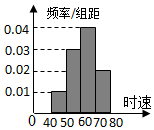 关于统计数据的分析,有以下几个结论:
关于统计数据的分析,有以下几个结论: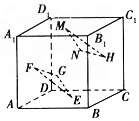 如图,在正方体ABCD-A1B1C1D1中中,E,F,G,H,M,N分别是正方体六个面的中心,求证:平面EFG∥平面HMN.
如图,在正方体ABCD-A1B1C1D1中中,E,F,G,H,M,N分别是正方体六个面的中心,求证:平面EFG∥平面HMN.