在等差数列{an}中.a4+a5+a6+a7=56.a4•a7=187.求a1和d．题目和参考答案——青夏教育精英家教网——

题目内容

11．在等差数列{a_n}中，a₄+a₅+a₆+a₇=56，a₄•a₇=187，求a₁和d．

分析利用等差数列的通项公式即可得出．

解答解：设等差数列{a_n}的公差为d，∵a₄+a₅+a₆+a₇=56，a₄•a₇=187，
∴4a₁+18d=56，（a₁+3d）（a₁+6d）=187，
解得$\left\{\begin{array}{l}{a_1}=5\\ d=2\end{array}\right.$或$\left\{\begin{array}{l}{a_1}=23\\ d=-2\end{array}\right.$

点评本题考查了等差数列的通项公式，考查了推理能力与计算能力，属于中档题．

练习册系列答案

名校课堂系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

相关题目

1．在圆x²+y²=4上任取一点P，过点P作x轴的垂线段PD，D为垂足，线段PD中点为M，当点P在圆上运动时，点M到直线l：x-y+1=0距离最大值为（　　）

$\frac{{\sqrt{10}+\sqrt{2}}}{2}$

$\frac{{\sqrt{10}-\sqrt{2}}}{2}$

$\frac{{3\sqrt{2}}}{2}$

$\frac{{\sqrt{2}}}{2}$

2．已知全集U=R，A={x|-2≤x≤4}，B={x|-3≤x≤3}，求（∁_UA）∩（∁_UB）=（　　）

{x|x＜-2或x＞4}

{x|x＜-3或x＞4}

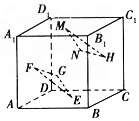如图，在正方体ABCD-A₁B₁C₁D₁中中，E，F，G，H，M，N分别是正方体六个面的中心，求证：平面EFG∥平面HMN．

6．计算下列各式的值：
（1）${0.027^{-\frac{1}{3}}}-{（-\frac{1}{7}）^{-2}}+{81^{\frac{3}{4}}}-{3^{-1}}+{（\sqrt{2}-1）^0}$
（2）log₃$\frac{{\root{4}{27}}}{3}+lg25+lg4+{7^{{{log}_7}2}}$．

16．已知集合A={x|1≤x≤5}，B={x|a＜x＜a+1}，若B⊆A，求实数a的取值范围．

3．已知f（x）是定义在（-1，1）上的偶函数，当x∈[0，1）时f（x）=lg$\frac{1}{1+x}$，
（1）求f（x）的解析式；
（2）探求f（x）的单调区间，并证明f（x）的单调性．

20．已知函数f（x）满足2f（1-x）-f（x-1）=x²-5x+2．
（1）求f（x）的解析式；
（2）已知a∈R，设P：M={x|x＜a}，N={x|-1＜x＜1}，且M∪（∁_RN）=R；Q：当x∈[-2，2]时，g（x）=f（x）-ax是单调函数，如果满足P成立的a的集合记为A，满足Q成立的a的集合记为B，求A∩∁_RB（其中R为全集）

1．已知命题：p：?x∈R，ax²+ax+1≥0，若￢p是真命题，则实数a的取值范围是（　　）

（-∞，0]∪[4，+∞）

（-∞，0）∪（4，+∞）