题目内容
10.已知等比数列{an}中,an+1=36,an+3=m,an+5=4,则圆锥曲线$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{3}$=1的离心率为( )| A. | $\sqrt{5}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{5}$或$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{5}}{2}$ |
分析 由等比数列{an}中,an+1=36,an+3=m,an+5=4,得m=±12,由此能求出圆锥曲线$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{3}$=1的离心率.
解答 解:∵等比数列{an}中,an+1=36,an+3=m,an+5=4,
∴m2=36×4,
∴m=±12.
m=-12,该圆锥曲线的方程为:$\frac{{x}^{2}}{-12}+\frac{{y}^{2}}{3}$=1,为焦点在y轴上的双曲线,其中a2=3,b2=12,
∴c2=a2+b2=15,离心率e=$\sqrt{5}$.
m=-2,该圆锥曲线的方程为:$\frac{{x}^{2}}{12}+\frac{{y}^{2}}{3}$=1,为焦点在x轴上的椭圆,其中a2=12,b2=3,
∴c2=a2-b2=9,离心率e=$\frac{\sqrt{3}}{2}$.
故选C.
点评 本题考查双曲线的简单性质,掌握双曲线的离心率的概念是基础,属于中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
2.若圆C1:(x-a)2+y2=4与圆C2:x2+(y-$\sqrt{5}$)2=a2相外切,则实数a的值为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{4}$或-$\frac{1}{4}$ | C. | $\frac{1}{2}$或-$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
19.某几何体的三视图如图所示,则该几何体的外接球的半径为( )
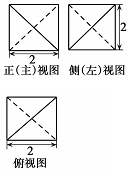

| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | $\sqrt{2}$ |
 如图,四棱锥D-ABCO的底面是直角梯形,已知OC∥AB,AB⊥BC,OA=OB,OD⊥DA,AB=2OC,OC=OD=BC=DA=1,DB=$\sqrt{3}$.
如图,四棱锥D-ABCO的底面是直角梯形,已知OC∥AB,AB⊥BC,OA=OB,OD⊥DA,AB=2OC,OC=OD=BC=DA=1,DB=$\sqrt{3}$.