题目内容
20．设集合A={2，0，11}，则集合A的真子集个数为7．分析 由集合A中的元素有3个，把n=3代入集合的真子集的公式2n-1中，即可计算出集合A真子集的个数．
解答 由集合A中的元素共3个，代入公式得：23-1=7，
故答案为：7，
点评 解得本题的关键是掌握当集合中元素有n个时，真子集的个数为2n-1．同时注意子集与真子集的区别：子集包含本身，而真子集不包含本身．
练习册系列答案
相关题目
10．已知等比数列{an}中，an+1=36，an+3=m，an+5=4，则圆锥曲线$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{3}$=1的离心率为（ ）
| A． | $\sqrt{5}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\sqrt{5}$或$\frac{\sqrt{3}}{2}$ | D． | $\frac{\sqrt{5}}{2}$ |
11．阅读如图的程序框图，运行相应的程序，则输出的值为（ ）
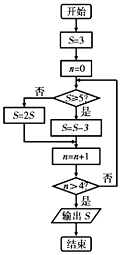
| A． | 3 | B． | 4 | C． | 6 | D． | 7 |
15．
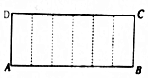已知矩形ABCD的周长为18，把它沿图中的虚线折成正六棱柱，当这个正六棱柱的体积最大时，它的外接球的表面积为（ ）
已知矩形ABCD的周长为18，把它沿图中的虚线折成正六棱柱，当这个正六棱柱的体积最大时，它的外接球的表面积为（ ）| A． | 13π | B． | 12π | C． | 11π | D． | 10π |
5．方程xy（x+y）=1所表示的曲线（ ）
| A． | 关于x轴对称 | B． | 关于y轴对称 | C． | 关于原点对称 | D． | 关于直线y=x对称 |
12．已知f（x）=$\left\{\begin{array}{l}{e^x}+a{x^2}，x＞0\\ \frac{1}{e^x}+a{x^2}，x＜0\end{array}$，若函数f（x）有四个零点，则实数a的取值范围是（ ）
| A． | （-∞，-e） | B． | （-∞，-$\frac{{e}^{2}}{4}$） | C． | （-∞，-$\frac{{e}^{3}}{9}$） | D． | （-∞，-$\frac{{e}^{4}}{16}$） |
9．已知函数f（x）=ex+$\frac{2x-5}{{x}^{2}+1}$的图象在点（0，f（0））处的切线与直线x-my+4=0垂直，则实数m的值为（ ）
| A． | -3 | B． | 3 | C． | -$\frac{1}{3}$ | D． | $\frac{1}{3}$ |