题目内容
2．若圆C1：（x-a）2+y2=4与圆C2：x2+（y-$\sqrt{5}$）2=a2相外切，则实数a的值为（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{4}$或-$\frac{1}{4}$ | C． | $\frac{1}{2}$或-$\frac{1}{2}$ | D． | $\frac{1}{2}$ |
分析 根据圆与圆之间的位置关系，两圆外切则圆心距等于半径之和，得到方程，求出a的值．
解答 解：由已知，
圆C1：（x-a）2+y2=4的圆心为C1（a，0），半径r1=2．
圆C2：x2+（y-$\sqrt{5}$）2=a2的圆心为C2（0，$\sqrt{5}$），半径r2=|a|．
∵圆C1：（x-a）2+y2=4与圆C2：x2+（y-$\sqrt{5}$）2=a2相外切，
∴|C1C2|=r1+r2．
∴$\sqrt{{a}^{2}+5}$=2+|a|，
∴a=$±\frac{1}{4}$，
故选B．
点评 本题考查圆与圆之间的位置关系，考查方程思想，属于基础题．
练习册系列答案
冲刺100分单元优化练考卷系列答案
相关题目
12．在数列{an}中，a1=-2，an+1=an-2n，则a2017的值为（ ）
| A． | 22016 | B． | 22018 | C． | -22017 | D． | 22017 |
13．已知函数f（x）（x∈R）满足f（x+π）=f（x）+cosx，当0≤x＜π时，f（x）=-1，则f（$\frac{2017π}{3}$）=（ ）
| A． | $\frac{1}{2}$ | B． | $-\frac{1}{2}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | -1 |
10．已知等比数列{an}中，an+1=36，an+3=m，an+5=4，则圆锥曲线$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{3}$=1的离心率为（ ）
| A． | $\sqrt{5}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\sqrt{5}$或$\frac{\sqrt{3}}{2}$ | D． | $\frac{\sqrt{5}}{2}$ |
17．过点P（2，-1）且倾斜角为$\frac{π}{4}$的直线方程是（ ）
| A． | x-y+1=0 | B． | $\sqrt{2}$x-2y-$\sqrt{2}$-2=0 | C． | x-y-3=0 | D． | $\sqrt{2}$x-2y+$\sqrt{2}$+1=0 |
14．若cos（$\frac{π}{2}+α$）=$\frac{3}{5}$，则cos2α=（ ）
| A． | $-\frac{7}{25}$ | B． | $\frac{7}{25}$ | C． | 一$\frac{16}{25}$ | D． | $\frac{16}{25}$ |
11．阅读如图的程序框图，运行相应的程序，则输出的值为（ ）
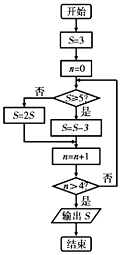
| A． | 3 | B． | 4 | C． | 6 | D． | 7 |
12．已知f（x）=$\left\{\begin{array}{l}{e^x}+a{x^2}，x＞0\\ \frac{1}{e^x}+a{x^2}，x＜0\end{array}$，若函数f（x）有四个零点，则实数a的取值范围是（ ）
| A． | （-∞，-e） | B． | （-∞，-$\frac{{e}^{2}}{4}$） | C． | （-∞，-$\frac{{e}^{3}}{9}$） | D． | （-∞，-$\frac{{e}^{4}}{16}$） |