题目内容
如图,直三棱柱ABCA1B1C1中, D,
D, E分别是AB,BB1的中点.
E分别是AB,BB1的中点.
(1)证明:BC1∥平面A1CD;
(2)设AA1=AC=CB=2,AB=2 ,求三棱锥CA1DE的体积.
,求三棱锥CA1DE的体积.
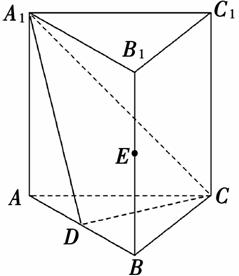
(1)证明:连接AC1交A1C于点F,则F为AC1中点,连接DF.

又D是AB中点,则BC1∥DF.
因为DF⊂平面A1CD,BC1⊄平面A1CD,所以BC1∥平面A1CD.
(2)解析:因为ABCA1B1C1是直三棱柱,所以AA1⊥CD.
又因为AC=CB,D为AB的中点,所以CD⊥AB.
又AA1∩AB=A,于是CD⊥平面ABB1A1.
由AA1=AC=CB=2,AB=2 得∠ACB=90°,CD=
得∠ACB=90°,CD= ,
,
A1D= ,DE=
,DE= ,A1E=3,
,A1E=3,
故A1D2+DE2=A1E2,即DE⊥A1D.
所以VC-A1DE= ×
× ×
× ×
× ×
× =1.
=1.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 :任意
:任意 ,有
,有 ,命题
,命题 :存在
:存在 ,使得
,使得 .若“
.若“ 或
或 为真”,“
为真”,“ 的取值范围.
的取值范围.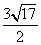 B.2
B.2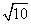 C.
C.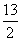 D.3
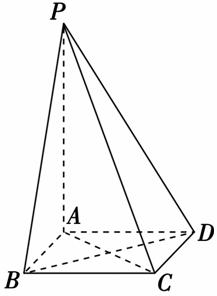
D.3 为2的正方形,PA⊥底面ABCD(如图)且PA=2
为2的正方形,PA⊥底面ABCD(如图)且PA=2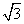 .
.


 另一个底面周长的3倍,轴截面的面积等于392,母线与轴的夹角为45°,求这个圆台的高、母线长和
另一个底面周长的3倍,轴截面的面积等于392,母线与轴的夹角为45°,求这个圆台的高、母线长和 (a>0且a≠1)是R上的减函数,则a的取值范围是
(a>0且a≠1)是R上的减函数,则a的取值范围是 ( )
( )

 D.
D. 
 ,若f(1)=-5,则f(f(5))=________________.
,若f(1)=-5,则f(f(5))=________________.