题目内容
若四棱锥PABCD的底面是边长 为2的正方形,PA⊥底面ABCD(如图)且PA=2
为2的正方形,PA⊥底面ABCD(如图)且PA=2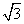 .
.
(1)求异面直线PD与BC所成角的大小;
(2)求四棱锥PABCD的体积.
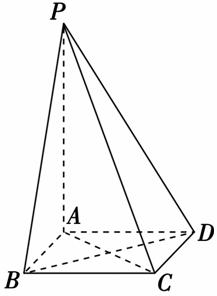
解析:(1)∵AD∥BC,∴∠PDA的大小即为异面直线PD与BC所成角的大小.
∵PA⊥平面ABCD,∴PA⊥AD,
由PA=2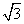 ,AD=2,得tan∠PDA=
,AD=2,得tan∠PDA=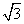 ,∴∠PDA=60°,
,∴∠PDA=60°,
故异面直线PD与BC所成角的大小为60°.
(2)∵PA⊥平面ABCD,
∴VP-ABCD=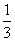 S正方形ABCD·PA=
S正方形ABCD·PA=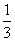 ×22×2
×22×2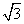 =
=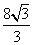 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在区间
在区间 内单调递增”的( )
内单调递增”的( )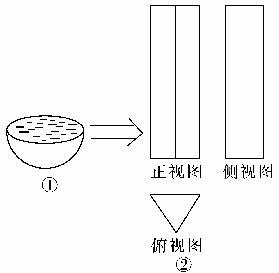
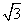 ≈1.732)
≈1.732)
 D,
D, E分别是AB,BB1的中点.
E分别是AB,BB1的中点. ,求三棱锥CA1DE的体积.
,求三棱锥CA1DE的体积.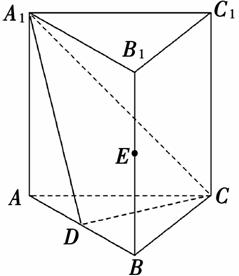
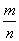 (m,n∈N*,m,n互质)的图象,则( )
(m,n∈N*,m,n互质)的图象,则( ) 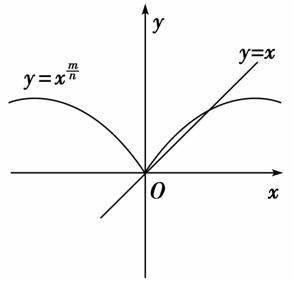
 >0的x的解集.
>0的x的解集.