题目内容
已知函数f(x)=x2-alnx,a∈R.
(Ⅰ) 讨论函数f(x)的单调性.
(Ⅱ)若f(x)在[1,+∞)上单调递增,求实数a的取值范围.
(Ⅰ) 讨论函数f(x)的单调性.
(Ⅱ)若f(x)在[1,+∞)上单调递增,求实数a的取值范围.
考点:利用导数研究函数的单调性
专题:计算题,函数的性质及应用,导数的综合应用
分析:(Ⅰ)先求函数f(x)的定义域为{x|x>0},再求导f′(x)=2x-
=
;从而讨论导数的正负以确定函数的单调性;
(Ⅱ)由f(x)在[1,+∞)上单调递增知f′(x)=
≥0在[1,+∞)上恒成立,从而化为最值问题.
| a |
| x |
| 2x2-a |
| x |
(Ⅱ)由f(x)在[1,+∞)上单调递增知f′(x)=
| 2x2-a |
| x |
解答:
解:(Ⅰ)f(x)的定义域为{x|x>0};
f′(x)=2x-
=
;
当a≤0时,f′(x)>0恒成立,
f(x)在(0,+∞)上递增;
当a>0时,x∈(0,
)时,f′(x)<0,f(x)单调递减,
x∈(
,+∞)时,f′(x)>0,f(x)单调递增.
(Ⅱ)∵f(x)在[1,+∞)上单调递增,
∴f′(x)=
≥0在[1,+∞)上恒成立,
∴a≤2x2,
即a≤2.
f′(x)=2x-
| a |
| x |
| 2x2-a |
| x |
当a≤0时,f′(x)>0恒成立,
f(x)在(0,+∞)上递增;
当a>0时,x∈(0,
| ||
| 2 |
x∈(
| ||
| 2 |
(Ⅱ)∵f(x)在[1,+∞)上单调递增,
∴f′(x)=
| 2x2-a |
| x |
∴a≤2x2,
即a≤2.
点评:本题考查了导数的综合应用及恒成立问题,属于中档题.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
一个人以6米/秒的速度去追赶停在交通灯前的汽车,当他离汽车25米时交通灯由红变绿,汽车开始变速直线行驶(汽车与人前进方向相同),汽车在时间t内的路程为s=
t2米,那么,此人( )
| 1 |
| 2 |
| A、可在7秒内追上汽车 |
| B、可在9秒内追上汽车 |
| C、不能追上汽车,但其间最近距离为14米 |
| D、不能追上汽车,但其间最近距离为7米 |
已知a>b>c>0,则a2+
+
+
的最小值为( )
| 1 |
| bc |
| 1 |
| a(a-b) |
| 1 |
| b(a-c) |
| A、4 | B、6 | C、8 | D、10 |
若半径均为2的四个球,每个球都与其他三个球外切,另有一个小球与这四个球都外切,则这个小球的半径为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
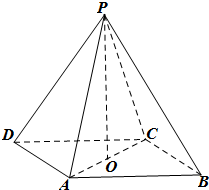 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAC=90°,O为AC的中点,PO⊥底面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAC=90°,O为AC的中点,PO⊥底面ABCD.