题目内容
14．已知曲线C：y=x3+5x2+3x．（1）求曲线C导函数．
（2）求曲线C在x=1处的切线方程．
分析 （1）利用导数公式，求曲线C导函数．
（2）求出切线斜率、切点坐标，即可求曲线C在x=1处的切线方程．
解答 解：（1）∵y=x3+5x2+3x，
∴y′=3x2+10x+3，
（2）切线斜率k=y′|x=1=16，当x=1时，y=9，
∴切线方程y-9=16（x-1），即16x-y-7=0．
点评 本题考查导数的几何意义以及导数的计算，涉及直线的点斜式方程，曲线上某点处的导数，就是曲线在该点的切线的斜率，是基础题．
练习册系列答案
开心试卷期末冲刺100分系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
8．设点A，B的坐标分别为（-6，0），（6，0），直线AM，BM相交于点M，且它们的斜率之积是$\frac{4}{9}$，则动点M的轨迹加上A，B两点所表示的曲线是（ ）
| A． | 圆 | B． | 椭圆 | C． | 抛物线 | D． | 双曲线 |
5．已知抛物线y2=6x的交点为F，准线为l，过点F的直线与抛物线交于点M，N，与l交于点P，若$\overrightarrow{MF}$=2$\overrightarrow{FN}$，O是坐标原点，则|OP|=（ ）
| A． | $\sqrt{13}$ | B． | $\sqrt{63}$ | C． | $\frac{4\sqrt{33}}{3}$ | D． | $\frac{3\sqrt{33}}{2}$ |
2．已知函数$y=sin（2x+\frac{π}{3}-2m）（m＞0）$为偶函数，则m的最小值为（ ）
| A． | $\frac{π}{12}$ | B． | $\frac{π}{3}$ | C． | $\frac{5π}{12}$ | D． | $\frac{7π}{12}$ |
19．等比数列{an}中，an＞0，a5a6=9，则log3a1+log3a2+log3a3+…+log3a10=（ ）
| A． | 12 | B． | 10 | C． | 8 | D． | 2+log35 |
6．
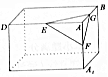如图，用小刀切一块长方体橡皮的一个角，在棱AD、AA1、AB上的截点分别是E、F、G，则截面△EFG（ ）
如图，用小刀切一块长方体橡皮的一个角，在棱AD、AA1、AB上的截点分别是E、F、G，则截面△EFG（ ）| A． | 一定是等边三角形 | B． | 一定是钝角三角形 | ||
| C． | 一定是锐角三角形 | D． | 一定是直角三角形 |
3．设函数f（x）=$\frac{{e}^{2}{x}^{2}+1}{x}$，g（x）=$\frac{{e}^{2}x}{{e}^{x}}$，对任意${x_1}，{x_2}∈（{\frac{1}{e}，+∞}）$，不等式$\frac{{g（{x_1}）}}{k}＜\frac{{f（{x_2}）}}{k+2}$恒成立，则正数k的取值范围是（ ）
| A． | （1，+∞） | B． | [1，+∞） | C． | （2，+∞） | D． | [2，+∞） |
4．已知A（-2，-1），B（2，-3），过点P（1，5）的直线l与线段AB有交点，则l的斜率的范围是（ ）
| A． | （-∞，-8] | B． | [2，+∞） | C． | （-∞，-8]∪[2，+∞） | D． | （-∞，-8）∪（2，+∞） |