题目内容
2.已知函数$y=sin(2x+\frac{π}{3}-2m)(m>0)$为偶函数,则m的最小值为( )| A. | $\frac{π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{12}$ | D. | $\frac{7π}{12}$ |
分析 利用诱导公式化简可得结论.
解答 解:函数$y=sin(2x+\frac{π}{3}-2m)(m>0)$为偶函数,
即$\frac{π}{3}-2m$=$\frac{π}{2}+kπ$,(k∈Z),
解得:m=$-\frac{π}{12}-\frac{1}{2}kπ$,
∵m>0,
当k=-1时,m取得最小值,即m=$\frac{5π}{12}$.
故选C.
点评 本题主要考查了正弦函数的奇偶性,由y函数$y=sin(2x+\frac{π}{3}-2m)(m>0)$是偶函数得到-2m+$\frac{π}{3}$=k$π+\frac{π}{2}$,k∈Z是解题的关键,属于基础题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目
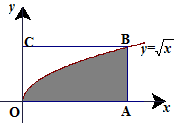 如图,长方形的四个顶点为O(0,2),A(4,0),B(4,2),C(0,2),曲线y=$\sqrt{x}$经过点B.现将一质点随机投入长方形OABC中,则质点落在图中阴影区域的概率是$\frac{2}{3}$.
如图,长方形的四个顶点为O(0,2),A(4,0),B(4,2),C(0,2),曲线y=$\sqrt{x}$经过点B.现将一质点随机投入长方形OABC中,则质点落在图中阴影区域的概率是$\frac{2}{3}$.