题目内容
已知定义在[-2,2]上的奇函数f(x)满足:当x∈(0,2]时,f(x)=x(x-2).
(1)求f(x)的解析式和值域;
(2)设g(x)=ln(x+2)-ax-2a,其中常数a>0.
①试指出函数F(x)=g(f(x))的零点个数;
②若当1+
是函数F(x)=g(f(x))的一个零点时,相应的常数a记为ak,其中k=1,2,…,n.
证明:a1+a2+…+an<
(n∈N*).
(1)求f(x)的解析式和值域;
(2)设g(x)=ln(x+2)-ax-2a,其中常数a>0.
①试指出函数F(x)=g(f(x))的零点个数;
②若当1+
| 1 |
| k |
证明:a1+a2+…+an<
| 7 |
| 6 |
考点:数列与函数的综合
专题:导数的综合应用,等差数列与等比数列
分析:(1)由奇函数性质得f(0)=0,当x∈[-2,0)时,f(x)=-f(-x)=-(-x)(-x-2)=-x(x+2),由此能求出f(x)的解析式和值域.
(2)①当t=0时,方程f(x)=t有三个实根,当t=1或t=-1时,方程f(x)=t只有一个实根,当t∈(0,1)或t∈(-1,0)时,方程f(x)=t有两个实根.设h(x)=
,x∈[-1,1],h(-1)=0,h′(x)=
,由此利用导数性质能求出函数F(x)=g(f(x))的零点个数.
②由已知得g(f(1+
))=0,g(f(1+
))=g(
-1)=ln(
+1-ak(
+1)=0,从而ak=
,记m(x)=ln(x+1)-x,m′(x)=
-1=
,由此利用导数性质能证明a1+a2+…+an<
(n∈N*).
(2)①当t=0时,方程f(x)=t有三个实根,当t=1或t=-1时,方程f(x)=t只有一个实根,当t∈(0,1)或t∈(-1,0)时,方程f(x)=t有两个实根.设h(x)=
| ln(x+2) |
| x+2 |
| 1-ln(x+2) |
| (x+2)2 |
②由已知得g(f(1+
| 1 |
| k |
| 1 |
| k |
| 1 |
| k2 |
| 1 |
| k2 |
| 1 |
| k2 |
ln(
| ||
|
| 1 |
| x+1 |
| -x |
| x+1 |
| 7 |
| 6 |
解答:
(1)解:∵f(x)为奇函数,∴f(0)=0.
当x∈[-2,0)时,-x∈(0,2],则f(x)=-f(-x)=-(-x)(-x-2)=-x(x+2),
∴f(x)=
.
∵x∈[0,2]时,f(x)∈[-1,0],x∈[-2,0),f(x)∈[0,1],
∴f(x)的值域为[-1,1].
(2)①解:函数f(x)的图象如图a所示,当t=0时,方程f(x)=t有三个实根,
当t=1或t=-1时,方程f(x)=t只有一个实根,
当t∈(0,1)或t∈(-1,0)时,方程f(x)=t有两个实根.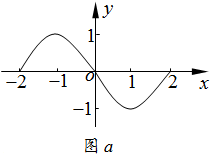
由g(x)=0,解得a=
,
∵f(x)的值域为[-1,1],
∴只需研究函数y=
在[-1,1]上的图象特征.
设h(x)=
,x∈[-1,1],h(-1)=0,
h′(x)=
,
令h′(x)=0,得x=e-2∈(0,1),h(e-2)=
.
∵当-1<x<e-2时,h′(x)>0,当e-2<x<1时,h′(x)<0,
又∵ln23<ln32,即
<
,
由h(0)=
,h(1)=
,得h(0)<h(1),
∴h(x)的大致图象如图b所示.
根据图象b可知,当0<a<
、
<a<
、a=
时,
直线y=a与函数y=h(x)的图象仅有一个交点,
则函数g(x)在[-1,1]上仅有一个零点,记零点为t,
则t分别在区间(-1,0)、(0,1)上,根据图象a,
方程f(x)=t有两个交点,
因此函数F(x)=g(f(x))有两个零点.
类似地,当a=
时,函数g(x)在[-1,1]上仅有零点0,
因此函数F(x)有-1、0、1这三个零点.
当a=
时,函数g(x)在[-1,1]上有两个零点,一个零点是1,
另一个零点在(0,1)内,因此函数Y(x)有三个零点.
当
<a<
时,函数g(x)在[-1,1]上有两个零点,
且这两个零点均在(0,1)内,因此函数F(x)有四个零点.
当a>
时,函数g(x)在[-1,1]上没有零点,因此函数F(x)没有零点.
②证明:∵1+
是函数F(x)=g(f(x))的一个零点,
∴有g(f(1+
))=0,∵1+
∈(0,2),∴f(1+
)=
-1,
∴g(f(1+
))=g(
-1)=ln(
+1-ak(
+1)=0,
∴ak=
,k=1,2,…,n.
记m(x)=ln(x+1)-x,m′(x)=
-1=
,
∵当x∈(0,1]时,m′(x)<0,
∴当x∈(0,1]时,m(x)<m(0)=0,即ln(x+1)<x.
故有ln(
+1)<
,则ak=
<
=
,k=1,2,…,n.
当n=1时,a1<
<
.
当n≥2时,∵
<
=
-
,
∴a1+a2+a3+…+an<
+
+
+…+
<
+(
-
)+(
-
)+…+(
-
)
=
+
-
=
-
<
.
综上,有a1+a2+…+an<
(n∈N*).
当x∈[-2,0)时,-x∈(0,2],则f(x)=-f(-x)=-(-x)(-x-2)=-x(x+2),
∴f(x)=
|
∵x∈[0,2]时,f(x)∈[-1,0],x∈[-2,0),f(x)∈[0,1],
∴f(x)的值域为[-1,1].
(2)①解:函数f(x)的图象如图a所示,当t=0时,方程f(x)=t有三个实根,
当t=1或t=-1时,方程f(x)=t只有一个实根,
当t∈(0,1)或t∈(-1,0)时,方程f(x)=t有两个实根.

由g(x)=0,解得a=
| ln(x+2) |
| x+2 |
∵f(x)的值域为[-1,1],
∴只需研究函数y=
| ln(x+2) |
| x+2 |
设h(x)=
| ln(x+2) |
| x+2 |
h′(x)=
| 1-ln(x+2) |
| (x+2)2 |
令h′(x)=0,得x=e-2∈(0,1),h(e-2)=
| 1 |
| e |
∵当-1<x<e-2时,h′(x)>0,当e-2<x<1时,h′(x)<0,
又∵ln23<ln32,即
| ln2 |
| 2 |
| ln3 |
| 3 |
由h(0)=
| ln2 |
| 2 |
| ln3 |
| 3 |
∴h(x)的大致图象如图b所示.

根据图象b可知,当0<a<
| ln2 |
| 2 |
| ln2 |
| 2 |
| ln3 |
| 3 |
| 1 |
| e |
直线y=a与函数y=h(x)的图象仅有一个交点,
则函数g(x)在[-1,1]上仅有一个零点,记零点为t,
则t分别在区间(-1,0)、(0,1)上,根据图象a,
方程f(x)=t有两个交点,
因此函数F(x)=g(f(x))有两个零点.
类似地,当a=
| ln2 |
| 2 |
因此函数F(x)有-1、0、1这三个零点.
当a=
| ln3 |
| 3 |
另一个零点在(0,1)内,因此函数Y(x)有三个零点.
当
| ln3 |
| 3 |
| 1 |
| e |
且这两个零点均在(0,1)内,因此函数F(x)有四个零点.
当a>
| 1 |
| e |
②证明:∵1+
| 1 |
| k |
∴有g(f(1+
| 1 |
| k |
| 1 |
| k |
| 1 |
| k |
| 1 |
| k2 |
∴g(f(1+
| 1 |
| k |
| 1 |
| k2 |
| 1 |
| k2 |
| 1 |
| k2 |
∴ak=
ln(
| ||
|
记m(x)=ln(x+1)-x,m′(x)=
| 1 |
| x+1 |
| -x |
| x+1 |
∵当x∈(0,1]时,m′(x)<0,
∴当x∈(0,1]时,m(x)<m(0)=0,即ln(x+1)<x.
故有ln(
| 1 |
| k2 |
| 1 |
| k2 |
ln(
| ||
|
| ||
|
| 1 |
| k2+1 |
当n=1时,a1<
| 1 |
| 2 |
| 7 |
| 6 |
当n≥2时,∵
| 1 |
| k2+1 |
| 1 | ||
k2-
|
| 2 |
| 2k-1 |
| 2 |
| 2k+1 |
∴a1+a2+a3+…+an<
| 1 |
| 12+1 |
| 1 |
| 22+1 |
| 1 |
| 32+1 |
| 1 |
| n2+1 |
<
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 7 |
| 2 |
| 2n-1 |
| 2 |
| 2n+1 |
=
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 2n+1 |
=
| 7 |
| 6 |
| 2 |
| 2n+1 |
| 7 |
| 6 |
综上,有a1+a2+…+an<
| 7 |
| 6 |
点评:本题主要考查函数的性质、分段函数、导数应用、一元二次方程的求解、连续函数的零点存在性定理,放缩法证明数列不等式,考查学生数形结合、分类讨论的数学思想,以及计算推理能力及分析问题、解决问题的能力及创新意识.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
三棱锥S-ABC的顶点都在同一球面上,且SA=AC=SB=BC=
,SC=2,则该球的体积为( )
| 2 |
A、
| ||
B、
| ||
| C、2π | ||
| D、8π |
已知正项数列{an}的前n项和为Sn,且2Sn=an+
,则S2015的值是( )
| 1 |
| an |
A、2015+
| ||||
B、2015-
| ||||
| C、2015 | ||||
D、
|
已知m,n表示两条不同直线,α表示平面,下列说法正确的是( )
| A、若m∥α,n∥α,则m∥n |
| B、若m⊥α,m⊥n,则n∥α |
| C、若m⊥α,n?α,则m⊥n |
| D、若m∥α,m⊥n,则n⊥α |
方程x2+
x-1=0的解可视为函数y=x+
的图象与函数y=
的图象交点的横坐标,若方程x4+ax-4=0各个实根x1,x2,…,xk(k≤4)所对应的点(xi,
)(i=1,2,…,k)均在直线y=x的同侧,则实数a的取值范围是( )
| 2 |
| 2 |
| 1 |
| x |
| 4 |
| xi |
| A、(-∞,-3) |
| B、(-3,3) |
| C、(3,∞) |
| D、(-∞,-6)∪(6,∞) |