题目内容

定义 A+B={x+y|x∈A，y∈B}，设集合 M={0，1+i}，N={0，
-1-3i
2+i
}，则集合 M+N中元素的个数为（　　）
A、4B、3C、2D、1
考点：元素与集合关系的判断
专题：集合,数系的扩充和复数
分析：先根据已知确定集合M中元素的属性，然后结合复数的运算求出各个元素即可．
解答： 解：因为
-1-3i
2+i
=-1-i，所以-1-i+1+i=0．
所以M+N={0，1+i，-1-i}．
共有3个元素．
故选B
点评：本题考查了元素与集合间的关系以及复数的运算，属于基础题．
练习册系列答案
相关题目
方程x2+
2
x-1=0的解可视为函数y=x+
2
的图象与函数y=
1
x
的图象交点的横坐标，若方程x4+ax-4=0各个实根x1，x2，…，xk（k≤4）所对应的点（xi，
4
xi
）（i=1，2，…，k）均在直线y=x的同侧，则实数a的取值范围是（　　）
A、（-∞，-3）
B、（-3，3）
C、（3，∞）
D、（-∞，-6）∪（6，∞）
设函数f（x）=x2-2ax（a＞0）．
（1）求函数在[0，2]上的最大值g（a）表达式；
（2）若a=1．函数在区间[m，n]的值域也是[m，n]（n＞m），求m，n 的值．
圆x2+y2+2y=1的圆心为（　　）
A、（0，1）
B、（0，-1）
C、（0，2）
D、（0，-2）
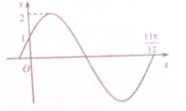
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
π
2
）的图象的第一部分如图所示，则（　　）
A、f（x）的最小正周期为2π
B、f（x）的图象关于直线x=
π
3
对称
C、f（x）的图线关于点（
5π
12
，0）对称
D、f（x）在[0，
π
2
]上是增函数
已知f（1，1）=1，f（m，n）∈N*（m，n∈N*），且对任意m，n∈N*都有：
①f（m，n+1）=f（m，n）+3；②f（m+1，1）=2f（m，1）
对于以下四个命题：
（1）数列{f（m，2015）}是等比数列；
（2）数列{f（2015，n）}是等差数列；
（3）f（1，1）+（1，2）+…+f（1，2015）=22015-1；
（4）f（1，1）+f（2，1）+…+f（2015，1）=22015-1；
其中真命题的序号为：
 
．
已知8个非零实数a1，a2，a3，…，a8，向量
OA1
=(a1，a2)，
OA2
=（a3，a4），
OA3
=（a5，a6），
OA4
=（a7，a8），对于下列命题：
①a1，a2，a3，…，a8为等差数列，则存在i，j（1≤i，j≤8，i≠j，i，j∈N*），使
4
k=1
OAk
与向量
n
=(ai，aj)共线；
②若a1，a2，a3，…，a8为公差不为0的等差数列，
n
=(ai，aj)（i≠j，i，j∈N*，1≤i，j≤8），
q
=(1，1)，M={y|y=
n
•
q
}，则集合M中元素有13个；
③若a1，a2，a3，…，a8为等比数列，则对任意i，j（1≤i，j≤4，i，j∈N*），都有
OAi
∥
OAj
；
④若a1，a2，a3，…，a8为等比数列，则存在i，j（1≤i，j≤4，i，j∈N*），使
OAi
•
OAj
＜0；
⑤若
m
=
OAi
•
OAj
（i≠j，1≤i，j≤4，i，j∈N*），则
m
的值中至少有一个不小于0．
上述命题正确的是
 
（填上所有正确命题的序号）
已知等差数列{an}共有2n-1项，则其奇数项之和与偶数项之和的比为（　　）
A、
n-1
n
B、
n+1
n
C、
n
n-1
D、
n+1
n-1
已知直线l过点（2，-6），它在y轴上的截距是在x轴上的截距的2倍，求直线l的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网