题目内容
4.已知抛物线C的顶点为O(0,0),焦点为F(0,1).(1)求抛物线C的方程;
(2)过点F的直线l:y=x+1交抛物线C于A,B两点,求三角形AOB的面积.
分析 (1)利用抛物线的顶点和焦点坐标,能求出抛物线C的标准方程.
(2)联立$\left\{\begin{array}{l}{{x}^{2}=4y}\\{y=x+1}\end{array}\right.$,得x2-4x-4=0,利用弦长公式求出|AB|,利用点到直线距离公式求出O(0,0)到直线y=x+1的距离d,由此能求出三角形AOB的面积.
解答 解:(1)∵抛物线C的顶点为O(0,0),焦点为F(0,1),
∴抛物线C的标准方程为:x2=4y.
(2)联立$\left\{\begin{array}{l}{{x}^{2}=4y}\\{y=x+1}\end{array}\right.$,得x2-4x-4=0,
设A(x1,y1),B(x2,y2),则x1+x2=4,x1x2=-4,
|AB|=$\sqrt{(1+1)(16+16)}$=8,
O(0,0)到直线y=x+1的距离d=$\frac{|1|}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
∴三角形AOB的面积S=$\frac{1}{2}×|AB|×d$=$\frac{1}{2}×8×\frac{\sqrt{2}}{2}$=2$\sqrt{2}$.
点评 本题考查抛物线方程的求法,考查三角形面积的求法,是基础题,解题时要认真审题,注意弦长公式、点到直线距离公式的合理运用.

练习册系列答案
相关题目
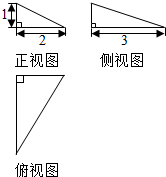
19.已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的体积是( )


| A. | 2 | B. | 4 | C. | 6 | D. | 12 |