题目内容
9.在正方体ABCD-A′B′C′D′中,判断下列命题是否正确,并说明理由:(1)直线AC在平面ABCD内;
(2)设上下底面中心为O,O′,则平面AA′C′C与平面BB′D′D的交线为OO′.
(3)点A,O,C′可以确定一平面.
(4)平面AB′C′与平面AC′D重合.
分析 (1)由题意可得A,C都在平面ABCD上,即可得解;
(2)利用正方体的性质解得O,O′两点都在平面AA′C′C与平面BB′D′D上,即可得证;
(3)根据平面公理,“过不在一条直线上的三点,有且只有一个平面”,即可得出答案;
(4)由AD∥B′C′,可得A,D,B′,C′四点共面,即可得证.
解答  解:(1)正确,
解:(1)正确,
∵A∈平面ABCD,C∈平面ABCD,
∴AC?平面ABCD.
(2)正确,
∵在正方体ABCD-A′B′C′D′中,AC∩BD=O,A′C′∩B′D′=O′,
∴O∈平面AA′C′C,O′∈平面AA′C′C,O′∈平面BB′D′D,O∈平面BB′D′D,
∴OO′?平面AA′C′C,OO′?平面BB′D′D,
∴平面AA′C′C与平面BB′D′D的交线为OO′.
(3)正确,
∵C′不在直线AO上,
∴点A,O,C′可以确定一平面.
(4)正确,
∵AD∥BC∥B′C′,
∴A,D,B′,C′四点共面,
∴平面AB′C′与平面AC′D重合.
点评 本题考查命题真假的判断,是基础题,解题时要认真审题,注意平面的基本性质及其推论的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.对抛物线y2=-12x,下列描述正确的是( )
| A. | 开口向下,焦点为(0,-3) | B. | 开口向上,焦点为(0,-3) | ||
| C. | 开口向左,焦点为(-3,0) | D. | 开口向右,焦点为(3,0) |
1.若f(x)=${∫}_{0}^{x}$|sin2t|dt(0<x<2π),则函数f(x)的单调递增区间为( )
| A. | (0,π) | B. | (0,2π) | C. | (0,t) | D. | (0,2t) |
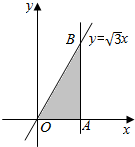 如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x,y=0,x=t(t>0)围成的△OAB的面积为S(t),则S(t)在t=2时的瞬时变化率是2$\sqrt{3}$.
如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x,y=0,x=t(t>0)围成的△OAB的面积为S(t),则S(t)在t=2时的瞬时变化率是2$\sqrt{3}$.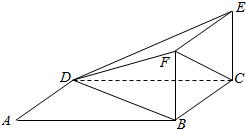 如图.ABCD为平行四边形,BCEF是边长为1的正方形.BF⊥BA,∠DAB=$\frac{π}{3}$,AB=2AD.
如图.ABCD为平行四边形,BCEF是边长为1的正方形.BF⊥BA,∠DAB=$\frac{π}{3}$,AB=2AD.