题目内容
13.某个几何体的三视图如图所示,则该几何体的体积是1.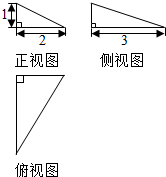
分析 该几何体为三棱锥,底面是直角三角形,高为1.
解答 解:由三视图可知该几何体为三棱锥,棱锥的底面为直角边为2和3的直角三角形,棱锥的高为1,
∴V=$\frac{1}{3}×\frac{1}{2}×2×3×1$=1.
故答案为:1.
点评 本题考查了三棱锥的结构特征和三视图,以及体积计算,属于基础题.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
1.若f(x)=${∫}_{0}^{x}$|sin2t|dt(0<x<2π),则函数f(x)的单调递增区间为( )
| A. | (0,π) | B. | (0,2π) | C. | (0,t) | D. | (0,2t) |
8.一个几何体的三视图如图所示,则该几何体的表面积为( )
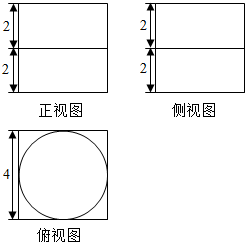

| A. | 64+8π | B. | 48+12π | C. | 48+8π | D. | 48+12π |
3.函数f(x)=2sin(ωx+$\frac{π}{4}$)(ω>0)与函数g(x)=cos(ωx+φ)(|φ|<$\frac{π}{2}$)的对称轴完全相同,则φ=( )
| A. | -$\frac{π}{4}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | -$\frac{π}{2}$ |
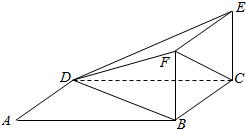 如图.ABCD为平行四边形,BCEF是边长为1的正方形.BF⊥BA,∠DAB=$\frac{π}{3}$,AB=2AD.
如图.ABCD为平行四边形,BCEF是边长为1的正方形.BF⊥BA,∠DAB=$\frac{π}{3}$,AB=2AD.