题目内容
12.下列五个命题中,①点P(-1,4)到直线3x+4y=2的距离为3.
②过点M(-3,5)且在两坐标轴上的截距互为相反数的直线方程为x-y+8=0.
③在正方体ABCD-A1B1C1D1中,E,F分别是AB,AD的中点,则异面直线B1C与EF所成的角的大小60°
④过点(-3,0)和点(-4,$\sqrt{3}$)的直线的倾斜角是120°
⑤直线x+2y+3=0与直线2x+4y+1=0的距离是$\frac{{\sqrt{5}}}{2}$.
其中正确的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 对5个选项分别进行判断,即可得出结论.
解答 解:①点P(-1,4)到直线3x+4y=2的距离为$\frac{|-3+16-2|}{5}$=2.2≠3,不正确.
②过点M(-3,5)且在两坐标轴上的截距互为相反数的直线方程为x-y+8=0或y=-$\frac{3}{5}$x,不正确.
③以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
设正方体ABCD-A1B1C1D1的棱长为2,
则E(2,1,0),F(1,0,0),B1(2,2,2),C(0,2,0),
∴$\overrightarrow{EF}$=(-1,-1,0),$\overrightarrow{{B}_{1}C}$=(-2,0,-2),
∴cos<$\overrightarrow{EF}$,$\overrightarrow{{B}_{1}C}$>=$\frac{1}{2}$,
∴异面直线B1C与EF所成的角的大小60°,正确
④过点(-3,0)和点(-4,$\sqrt{3}$)的直线的斜率为-$\sqrt{3}$,倾斜角是120°,正确;
⑤直线x+2y+3=0与直线2x+4y+1=0的距离是$\frac{|6-1|}{\sqrt{4+16}}$=$\frac{{\sqrt{5}}}{2}$,正确.
故选:C.
点评 本题考查命题的真假判断,考查直线方程,点到直线的距离公式,直线的倾斜角,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
1.若f(x)=${∫}_{0}^{x}$|sin2t|dt(0<x<2π),则函数f(x)的单调递增区间为( )
| A. | (0,π) | B. | (0,2π) | C. | (0,t) | D. | (0,2t) |
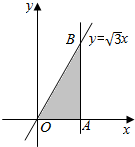 如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x,y=0,x=t(t>0)围成的△OAB的面积为S(t),则S(t)在t=2时的瞬时变化率是2$\sqrt{3}$.
如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x,y=0,x=t(t>0)围成的△OAB的面积为S(t),则S(t)在t=2时的瞬时变化率是2$\sqrt{3}$.