题目内容

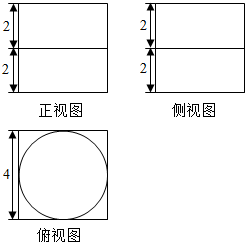
19．已知一个空间几何体的三视图如图所示，根据图中标出的尺寸，可得这个几何体的体积是（　　）
A．2B．4C．6D．12

分析 几何体为四棱锥，棱锥高为2，底面为梯形，代入体积公式计算．

解答 解：由三视图可知该几何体为四棱锥，棱锥的底面是直角梯形，棱锥的高是2，
∴V=$\frac{1}{3}×\frac{1}{2}×（2+4）×2×2$=4．
故选B．

点评 本题考查了空间几何体的三视图和体积计算，属于基础题．

练习册系列答案
相关题目
9．已知等比数列{an}满足a2=1，${a_3}{a_5}=6（{a_4}-\frac{3}{2}）$，则a6=（　　）
A．3B．6C．9D．18
10．已知命题“设a，b，c∈R，如果ac2＞bc2，则a＞b”，则它的逆命题、否命题和逆否命题中真命题的个数为1．
7．已知向量$\overrightarrow a=（2x，1，3）$，向量$\overrightarrow b=（1，-2y，9）$，若$\overrightarrow a$与$\overrightarrow b$共线，则x=-$\frac{1}{6}$，y=-$\frac{3}{2}$．
14．由曲线xy=1，直线y=x，x=3所围成的封闭图形的面积为（　　）
A．$\frac{1}{2}+ln3$B．4-ln3C．$\frac{9}{2}$D．$\frac{11}{6}$
4．已知抛物线C的顶点为O（0，0），焦点为F（0，1）．
（1）求抛物线C的方程；
（2）过点F的直线l：y=x+1交抛物线C于A，B两点，求三角形AOB的面积．
11．用一平面去截割一圆柱，所得几何体的三视图如图所示，则该几何体的体积为（　　）
A．36πB．45πC．48πD．72π
8．一个几何体的三视图如图所示，则该几何体的表面积为（　　）
A．64+8πB．48+12πC．48+8πD．48+12π
9．已知函数f（x）=ax2+bx+c满足f（1）=0，且a＞b＞c．
（1）求$\frac{c}{a}$的取值范围；
（2）设该函数图象交x轴于A、B两点，求AB的范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网