题目内容
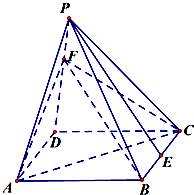 如图,在正四棱锥P-ABCD中,底面是边长为2的正方形,侧棱PA=
如图,在正四棱锥P-ABCD中,底面是边长为2的正方形,侧棱PA=| 6 |
E为BC的中点,F是侧棱PD上的一动点.
(1)证明:AC⊥BF;
(2)当直线PE∥平面ACF时,求三棱锥F-ACD的体积.
考点:棱柱、棱锥、棱台的体积,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:(1)得出PO⊥面ABCD,AC⊥PO,AC⊥面PBD,判断即可AC⊥BF,
(2)得出比例线段
=
,
=
=
,
=
,运用体积公式求解即可vF-ACD=
S△ACD•FH
(2)得出比例线段
| DG |
| DE |
| DF |
| DP |
| EC |
| AD |
| GE |
| DG |
| 1 |
| 2 |
| DG |
| DE |
| 2 |
| 3 |
| 1 |
| 3 |
解答:
解:(1)连接BD,设AC∩BD=0,连接PO,
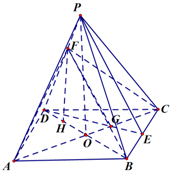
则PO⊥面ABCD,
∴AC⊥PO,
∵四边形ABCD为正方形,
∴AC⊥BD,BD∩OP=O
∴AC⊥面PBD,∴AC⊥BF,
(2)连接DE交AC于G点,连接FG,
∵PE∥平面ACF,∴PE∥FG
∴
=
,
又CE=
BC=
AD,BC∥AD
∴
=
=
,∴
=
,
过F作FH⊥DB垂足为H则FH∥OP
∴
=
=
,
∴FH=
OP=
∴vF-ACD=
S△ACD•FH=
×
×22×
=
.

则PO⊥面ABCD,
∴AC⊥PO,
∵四边形ABCD为正方形,
∴AC⊥BD,BD∩OP=O
∴AC⊥面PBD,∴AC⊥BF,
(2)连接DE交AC于G点,连接FG,
∵PE∥平面ACF,∴PE∥FG
∴
| DG |
| DE |
| DF |
| DP |
又CE=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| EC |
| AD |
| GE |
| DG |
| 1 |
| 2 |
| DG |
| DE |
| 2 |
| 3 |
过F作FH⊥DB垂足为H则FH∥OP
∴
| FH |
| OP |
| DF |
| DP |
| 2 |
| 3 |
∴FH=
| 2 |
| 3 |
| 4 |
| 3 |
∴vF-ACD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
| 8 |
| 9 |
点评:本题考查了空间几何体的性质,线面的垂直,体积的求解,属于中档题,关键是确定几何题的高,底面积,难度不大.

练习册系列答案
相关题目
已知函数f(x)=
,若不等式f(x)<0的解集为非空集合D,且D⊆(-1,2),则z=2a-b的取值范围为( )
|
| A、(4,+∞) |
| B、[-4,+∞) |
| C、(-∞,4) |
| D、(-1,4) |
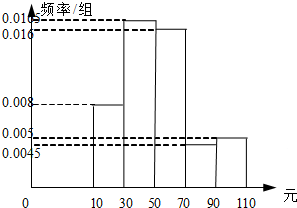
 甲、乙两位同学在相同的5次数学测试中,测试成绩如图所示,设
甲、乙两位同学在相同的5次数学测试中,测试成绩如图所示,设