题目内容
13.关于x的函数y=log${\;}_{\frac{1}{2}}$(x2-ax+2a)在[1,+∞)上为减函数,则实数a的取值范围是( )| A. | (-∞,2] | B. | (-1,+∞) | C. | (-1,2] | D. | (-∞,-1) |
分析 由题意可得,t=x2-ax+2a)在[1,+∞)上为增函数,且在[1,+∞)上大于0恒成立,得到关于a的不等式组求解.
解答 解:∵函数y=log${\;}_{\frac{1}{2}}$(x2-ax+2a)在[1,+∞)上为减函数,
则t=x2-ax+2a)在[1,+∞)上为增函数,且在[1,+∞)上大于0恒成立.
则$\left\{\begin{array}{l}{\frac{a}{2}≤1}\\{{1}^{2}-a+2a>0}\end{array}\right.$,解得-1<a≤2.
∴实数a的取值范围是(-1,2].
故选:C.
点评 本题主要考查了复合函数的单调性以及单调区间的求法.对应复合函数的单调性,一要注意先确定函数的定义域,二要利用复合函数与内层函数和外层函数单调性之间的关系进行判断,判断的依据是“同增异减”,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.已知向量|$\overrightarrow{a}$|=$\sqrt{5}$,$\overrightarrow{a}$•$\overrightarrow{b}$=10,|$\overrightarrow{a}$+$\overrightarrow{b}$|=5$\sqrt{2}$,则|$\overrightarrow{b}$|=( )
| A. | $\sqrt{5}$ | B. | $\sqrt{10}$ | C. | 5 | D. | 25 |
5.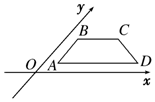 用斜二测画法画出的某平面图形的直观图如图,边AB平行于y轴,BC,AD平行于x轴.已知四边形ABCD的面积为2$\sqrt{2}$ cm2,则原平面图形的面积为( )
用斜二测画法画出的某平面图形的直观图如图,边AB平行于y轴,BC,AD平行于x轴.已知四边形ABCD的面积为2$\sqrt{2}$ cm2,则原平面图形的面积为( )
 用斜二测画法画出的某平面图形的直观图如图,边AB平行于y轴,BC,AD平行于x轴.已知四边形ABCD的面积为2$\sqrt{2}$ cm2,则原平面图形的面积为( )
用斜二测画法画出的某平面图形的直观图如图,边AB平行于y轴,BC,AD平行于x轴.已知四边形ABCD的面积为2$\sqrt{2}$ cm2,则原平面图形的面积为( )| A. | 4 cm2 | B. | 4$\sqrt{2}$ cm2 | C. | 8 cm2 | D. | 8$\sqrt{2}$ cm2 |
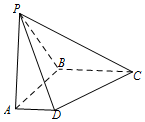 如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面ABCD,PA=AB=BC=3,梯形上底AD=1.
如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面ABCD,PA=AB=BC=3,梯形上底AD=1.