题目内容
18．已知集合A={x|x＜-1或x≥1}，B={x|2a＜x≤a+1，a＜1}，A∪B=A，求实数a的取值范围．分析 由已知得B?A，根据B=∅和B≠∅两种情况分类讨论能求出实数a的取值范围．
解答 解：∵集合A={x|x＜-1或x≥1}，B={x|2a＜x≤a+1，a＜1}，A∪B=A，
∴B?A，
当B=∅时，a+1≤2a，且a＜1，解得a≥1，不成立；
当B≠∅时，$\left\{\begin{array}{l}{a＜1}\\{2a≥1}\end{array}\right.$或$\left\{\begin{array}{l}{a＜1}\\{a+1≤-1}\end{array}\right.$，
解得$\frac{1}{2}≤a＜1$或a≤-2．
∴实数a的取值范围是[$\frac{1}{2}，1$）∪（-∞，-2]．
点评 本题考查实数值的求法，是基础题，解题时要认真审题，注意并集性质的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
8．
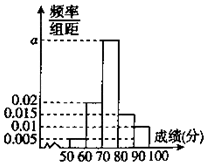为了了解某学校高二年级学生的物理成绩，从中抽取n名学生的物理成绩（百分制）作为样本，按成绩分成 5组：[50，60），[60，70），[70，80），[80，90），[90，100]，频率分布直方图如图所示，成绩落在[70，80）中的人数为20．
（1）求a和n的值；
（2）设成绩在80分以上（含80分）为优秀，已知样本中成绩落在[50，80）中的男、女生人数比为1：2，成绩落在[80，100]中的男、女生人数比为3：2，请完成下面的2×2列联表，并判断是否有95%的把握认为物理成绩优秀与性别有关．
参考公式和数据：K2=$\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$
为了了解某学校高二年级学生的物理成绩，从中抽取n名学生的物理成绩（百分制）作为样本，按成绩分成 5组：[50，60），[60，70），[70，80），[80，90），[90，100]，频率分布直方图如图所示，成绩落在[70，80）中的人数为20．（1）求a和n的值；
（2）设成绩在80分以上（含80分）为优秀，已知样本中成绩落在[50，80）中的男、女生人数比为1：2，成绩落在[80，100]中的男、女生人数比为3：2，请完成下面的2×2列联表，并判断是否有95%的把握认为物理成绩优秀与性别有关．
参考公式和数据：K2=$\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$
| P（K2≥k） | 0.50 | 0.05 | 0.025 | 0.005 |
| k | 0.455 | 3.841 | 5.024 | 7.879 |
| 男生 | 女生 | 合计 | |
| 优秀 | |||
| 不优秀 | |||
| 合计 |
6．集合A={x|-2＜x＜3}，B={x∈Z|x2-5x＜0}，则A∩B=（ ）
| A． | {1，2} | B． | {2，3} | C． | {1，2，3} | D． | {2，3，4} |
13．关于x的函数y=log${\;}_{\frac{1}{2}}$（x2-ax+2a）在[1，+∞）上为减函数，则实数a的取值范围是（ ）
| A． | （-∞，2] | B． | （-1，+∞） | C． | （-1，2] | D． | （-∞，-1） |
10．若函数f（x）=sin（2x+φ）满足?x∈R，f（x）≤f（$\frac{π}{6}$），则f（x）在[0，π]上的单调递增区间为（ ）
| A． | [0，$\frac{π}{6}$]与[$\frac{π}{2}$，$\frac{2π}{3}$] | B． | [$\frac{π}{3}$，$\frac{2π}{3}$] | C． | [0，$\frac{π}{6}$]与[$\frac{2π}{3}$，π] | D． | [0，$\frac{π}{6}$]与[$\frac{π}{3}$，$\frac{2π}{3}$] |
7．下列所示的四幅图中，是函数图象的是（ ）
| A． |  | B． |  | C． |  | D． |  |