题目内容
3.已知平面α∥平面β,A,C∈α,B,D∈β,直线AB与CD交于点S,且AS=9,BS=8,CD=34,(1)当S在α,β之间时,CS长多少?
(2)当S不在α,β之间时,CS长又是多少?
分析 由平面α∥平面β,且A、C∈α,B、D∈β,直线AB与CD交于点S,根据平面与平面平行的性质定理可得:两条交线应该平行,连接AC、BD,即AC∥BD,则△SAC∽△SBD,又根据相似比的概念及AS=9,BS=8,CD=34,可得:(1)SC=18;(2)SC=306.
解答 解:∵平面α∥平面β,A、C∈α,B、D∈β,直线AB与CD交于点S,
∴根据平面与平面平行的性质定理可得:AC∥BD,
∴△SAC∽△SBD,
(1)$\frac{SC}{SD}=\frac{AS}{SB}$=$\frac{9}{8}$,且SC+SD=CD=34,
则:SC=18;
(2)$\frac{SC}{SD}=\frac{AS}{SB}=\frac{9}{8}$,且SC-SD=CD=34,
则:SC=306.
点评 本题主要考查了空间中直线与平面平行的性质,相似三角形的判定,考查空间想象能力和思维能力,是中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
2.下列函数中,在区间(0,2)上为增函数的是( )
| A. | y=-2x+1 | B. | y=$\frac{1}{3}$x2+1 | C. | y=-x2-x-1 | D. | y=x2-x+1 |
11.${∫}_{-1}^{1}$x2dx=( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
8.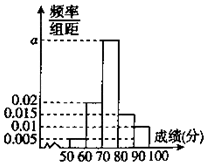 为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成 5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示,成绩落在[70,80)中的人数为20.
为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成 5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示,成绩落在[70,80)中的人数为20.
(1)求a和n的值;
(2)设成绩在80分以上(含80分)为优秀,已知样本中成绩落在[50,80)中的男、女生人数比为1:2,成绩落在[80,100]中的男、女生人数比为3:2,请完成下面的2×2列联表,并判断是否有95%的把握认为物理成绩优秀与性别有关.
参考公式和数据:K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
 为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成 5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示,成绩落在[70,80)中的人数为20.
为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成 5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示,成绩落在[70,80)中的人数为20.(1)求a和n的值;
(2)设成绩在80分以上(含80分)为优秀,已知样本中成绩落在[50,80)中的男、女生人数比为1:2,成绩落在[80,100]中的男、女生人数比为3:2,请完成下面的2×2列联表,并判断是否有95%的把握认为物理成绩优秀与性别有关.
参考公式和数据:K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k) | 0.50 | 0.05 | 0.025 | 0.005 |
| k | 0.455 | 3.841 | 5.024 | 7.879 |
| 男生 | 女生 | 合计 | |
| 优秀 | |||
| 不优秀 | |||
| 合计 |
13.关于x的函数y=log${\;}_{\frac{1}{2}}$(x2-ax+2a)在[1,+∞)上为减函数,则实数a的取值范围是( )
| A. | (-∞,2] | B. | (-1,+∞) | C. | (-1,2] | D. | (-∞,-1) |
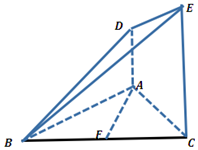 如图,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1,四边形ACED的面积为$\frac{3}{2}$,F为BC的中点,
如图,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1,四边形ACED的面积为$\frac{3}{2}$,F为BC的中点,