题目内容
13.我国古代数学名著《九章算术》中,有已知长方形面积求一边的算法,其方法的前两步为:第一步:构造数列1,$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{4}$,…,$\frac{1}{n}$.①
第二步:将数列①的各项乘以n,得到数列(记为)a1,a2,a3,…,an.则a1a2+a2a3+…+an-1an=( )
| A. | n2 | B. | (n-1)2 | C. | n(n-1) | D. | n(n+1) |
分析 ak=$\frac{n}{k}$.n≥2时,ak-1ak=$\frac{{n}^{2}}{(k-1)k}$=n2$(\frac{1}{k-1}-\frac{1}{k})$.利用“裂项求和”方法即可得出.
解答 解:∵ak=$\frac{n}{k}$.
n≥2时,ak-1ak=$\frac{{n}^{2}}{(k-1)k}$=n2$(\frac{1}{k-1}-\frac{1}{k})$.
∴a1a2+a2a3+…+an-1an=n2$[(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{n-1}-\frac{1}{n})]$
=${n}^{2}(1-\frac{1}{n})$=n(n-1).
故选:C.
点评 本题考查了“裂项求和”方法、数列通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
3.设函数f(x)=$\frac{{4}^{x}}{{4}^{x}+1}$,若[x]表示不超过x的最大整数,则函数y=[f(x)-$\frac{1}{2}$]+[f(x)+$\frac{1}{2}$]的值域是( )
| A. | {0,-1} | B. | {0,1} | C. | {-1,1} | D. | {-1,0,1} |
4.已知扇形的面积为5,周长为9,则该扇形的圆心角为( )
| A. | $\frac{5}{2}$ | B. | $\frac{8}{5}$ | C. | $\frac{5}{2}$或$\frac{8}{5}$ | D. | $\frac{5}{2}$或$\frac{4}{5}$ |
1.若a=log23,b=2.11.1,c=lg2+lg5,则a,b,c的大小关系为( )
| A. | b>a>c | B. | a>b>c | C. | c>b>a | D. | 无法确定 |
5.曲线y=1+$\sqrt{4-{x}^{2}}$与直线kx-y-2k+4=0有两个交点时,实数k取值范围是( )
| A. | ($\frac{5}{12}$,$\frac{3}{4}$] | B. | ($\frac{5}{12}$,$\frac{3}{4}$) | C. | ($\frac{1}{3}$,$\frac{3}{4}$] | D. | (0,$\frac{5}{12}$) |
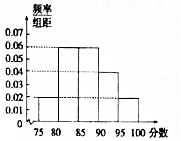 某校为了了解高三学生体育达标情况,在高三学生体育达标成绩中随机抽取50个进行调研,按成绩分组:第l组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示:若要在成绩较高的第3,4,5组中用分层抽样抽取6名学生进行复查:
某校为了了解高三学生体育达标情况,在高三学生体育达标成绩中随机抽取50个进行调研,按成绩分组:第l组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示:若要在成绩较高的第3,4,5组中用分层抽样抽取6名学生进行复查: