题目内容
8.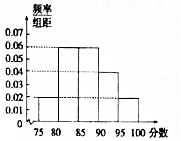 某校为了了解高三学生体育达标情况,在高三学生体育达标成绩中随机抽取50个进行调研,按成绩分组:第l组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示:若要在成绩较高的第3,4,5组中用分层抽样抽取6名学生进行复查:
某校为了了解高三学生体育达标情况,在高三学生体育达标成绩中随机抽取50个进行调研,按成绩分组:第l组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示:若要在成绩较高的第3,4,5组中用分层抽样抽取6名学生进行复查:(1)已知学生甲的成绩在第5组,求学生甲被抽中复查的概率;
(2)在已抽取到的6名学生中随机抽取2名学生接受篮球项目的考核,求其中一人在第3组,另一人在第4组的概率.
分析 (1)设“学生甲被选中复查”为事件A,根据分层抽样的方法求出每组的人数,即可求出P(A);
(2)记第3组选中的3人分别是a,b,c,第4组选中的2人分别为x,y,第五组选中的人为m,用列举法计算基本事件数,求出概率即可.
解答 解:(1)设“学生甲被选中复查”为事件A,
第三组人数为50×0.06×5=15,
第四组人数为50×0.04×5=10,
第五组人数为50×0.02×5=5,
根据分层抽样知,第三组应抽取3人,第四组应抽取2人,第五组应抽取1人,
所以P(A)=$\frac{1}{5}$;
(2)记第三组选中的三人分别是a,b,c,第四组选中的二人分别为x,y,第五组选中的人为m,
从这六人中选出两人,有以下基本事件:
ab,ac,ax,ay,am,bc,bx,by,bm,cx,cy,cm,xy,xm,ym,共15个基本事件,
符合1人在第3组1人在第4组的基本事件有ax,ay,bx,by,cx,cy,共6个,
故所求的概率为P=$\frac{6}{15}$=$\frac{2}{5}$.
点评 本题考查了分层抽样以及列举法求概率的应用问题,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.如果点P(sin2θ,2cosθ)位于第三象限,那么角θ所在的象限是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
16.设函数f(x)=sin(2x+$\frac{π}{3}$),则下列关于函数f(x)的说法中正确的是( )
| A. | f(x)是偶函数 | B. | f(x)最小正周期为2π | ||
| C. | f(x)图线关于直线点x=-$\frac{π}{6}$对称 | D. | f(x)图象关于点(-$\frac{π}{6}$,0)对称 |
3.为了得到函数y=2sin(2x-$\frac{π}{3}$)的图象,只需把函数y=2sinx(2x+$\frac{π}{6}$)的图象上所有的点( )
| A. | 向左平行平移$\frac{π}{2}$个单位长度 | B. | 向右平行平移$\frac{π}{4}$个单位长度 | ||
| C. | 向右平行平移$\frac{π}{2}$个单位长度 | D. | 向左平行平移$\frac{π}{4}$个单位长度 |
13.我国古代数学名著《九章算术》中,有已知长方形面积求一边的算法,其方法的前两步为:
第一步:构造数列1,$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{4}$,…,$\frac{1}{n}$.①
第二步:将数列①的各项乘以n,得到数列(记为)a1,a2,a3,…,an.则a1a2+a2a3+…+an-1an=( )
第一步:构造数列1,$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{4}$,…,$\frac{1}{n}$.①
第二步:将数列①的各项乘以n,得到数列(记为)a1,a2,a3,…,an.则a1a2+a2a3+…+an-1an=( )
| A. | n2 | B. | (n-1)2 | C. | n(n-1) | D. | n(n+1) |
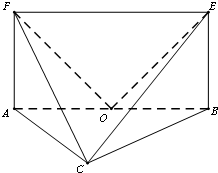 如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC,O为AB的中点,OF⊥EC.
如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC,O为AB的中点,OF⊥EC.