题目内容
3．△ABC的内角 A、B、C 的对边分别为a、b、c，已知A=$\frac{π}{3}$，a=2$\sqrt{21}$，b=10，则c=（ ）| A． | 2 或8 | B． | 2 | C． | 8 | D． | 21 |
分析 根据正弦定理求出sinB，从而求出cosB，根据两角和的正弦公式求出sinC，从而求出c的值即可．
解答 解：∵$\frac{a}{sinA}$=$\frac{b}{sinB}$，
∴$\frac{2\sqrt{21}}{sin\frac{π}{3}}$=$\frac{10}{sinB}$，
解得：sinB=$\frac{5}{2\sqrt{7}}$，
故cosB=±$\frac{\sqrt{3}}{2\sqrt{7}}$，
故sinC=sin（A+B）=$\frac{2}{\sqrt{7}}$或$\frac{1}{2\sqrt{7}}$，
由$\frac{a}{sinA}$=$\frac{c}{sinC}$，
得：c=$\frac{asinC}{sinA}$=$\frac{2\sqrt{21}×\frac{2}{\sqrt{7}}}{\frac{\sqrt{3}}{2}}$=8，
或c=$\frac{2\sqrt{21}×\frac{1}{2\sqrt{7}}}{\frac{\sqrt{3}}{2}}$=2，
故选：A．
点评 本题考查了正弦定理，考查两角和的正弦公式，是一道基础题．
练习册系列答案
相关题目
13．我国古代数学名著《九章算术》中，有已知长方形面积求一边的算法，其方法的前两步为：
第一步：构造数列1，$\frac{1}{2}$，$\frac{1}{3}$，$\frac{1}{4}$，…，$\frac{1}{n}$．①
第二步：将数列①的各项乘以n，得到数列（记为）a1，a2，a3，…，an．则a1a2+a2a3+…+an-1an=（ ）
第一步：构造数列1，$\frac{1}{2}$，$\frac{1}{3}$，$\frac{1}{4}$，…，$\frac{1}{n}$．①
第二步：将数列①的各项乘以n，得到数列（记为）a1，a2，a3，…，an．则a1a2+a2a3+…+an-1an=（ ）
| A． | n2 | B． | （n-1）2 | C． | n（n-1） | D． | n（n+1） |
14．已知全集U={1，2，3，4，5}，集合A={3，4}，B={1，2}，则（∁UA）∩B等于（ ）
| A． | {1，2} | B． | [1，3} | C． | {1，2，5} | D． | {1，2，3} |
11．经过点A（-1，4）且在x轴上的截距为3的直线方程是（ ）
| A． | x+y+3=0 | B． | x-y+5=0 | C． | x+y-3=0 | D． | x+y-5=0 |
8．
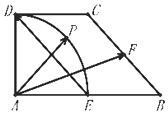在直角梯形 ABCD 中，AB⊥AD，DC∥AB，AD=DC=1，AB=2，E，F 分别为
AB，AC 的中点，以A 为圆心，AD为半径的圆弧DE中点为P （如图所示）．
若$\overrightarrow{AP}=λ\overrightarrow{ED}+μ\overrightarrow{AF}$，其中λ，μ∈R，则λ+μ的值是（ ）
在直角梯形 ABCD 中，AB⊥AD，DC∥AB，AD=DC=1，AB=2，E，F 分别为AB，AC 的中点，以A 为圆心，AD为半径的圆弧DE中点为P （如图所示）．
若$\overrightarrow{AP}=λ\overrightarrow{ED}+μ\overrightarrow{AF}$，其中λ，μ∈R，则λ+μ的值是（ ）
| A． | $\frac{{\sqrt{2}}}{2}$ | B． | $\frac{{3\sqrt{2}}}{4}$ | C． | $\sqrt{2}$ | D． | $\frac{3}{4}$ |
15．已知集合A={1，3，5}，B={1，m}，A∩B={1，m}，则m等于（ ）
| A． | 1 或 3 | B． | 3 或 5 | C． | 1 或 5 | D． | 1 或 3 或5 |
12．在空间直角坐标系Oxyz中，z轴上的点M到点A（1，0，2）与点B（1，-3，1）的距离相等，则点M的坐标是（ ）
| A． | （0，0，-3） | B． | （0，0，3） | C． | （0，0，$\sqrt{10}$） | D． | （0，0，-$\sqrt{10}$） |