题目内容
如果椭圆
+y2=k上两点间的距离最大值为8，则k的值为（ ）
| x2 |
| 4 |
| A、32 | B、16 | C、8 | D、4 |
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：根据椭圆上两点间的最大距离为长轴2a，即可求出k的值．
解答：
解：∵在椭圆
+y2=k中，
标准方程为
+
=1，
∴该椭圆上两点间的最大距离为2
=8，
解得k=4．
故选：D．
| x2 |
| 4 |
标准方程为
| x2 |
| 4k |
| y2 |
| k |
∴该椭圆上两点间的最大距离为2
| 4k |
解得k=4．
故选：D．
点评：本题考查了椭圆的标准方程与几何性质的应用问题，是基础题目．
练习册系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
A加金题 系列答案
相关题目
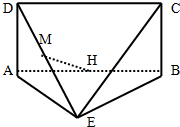已知平面ABCD⊥平面ABE，四边形ABCD是矩形，AD=AE=BE=2，M、H分别是DE、AB的中点，主（正）视图方向垂直平面ABCD时，左（侧）视图的面积为