题目内容
已知直线l1:2x+(m+1)y-2=0;直线l2:mx+y-1=0.
(Ⅰ)若l1⊥l2求实数m的值.
(Ⅱ)若l1∥l2,求实数m的值.
(Ⅰ)若l1⊥l2求实数m的值.
(Ⅱ)若l1∥l2,求实数m的值.
考点:直线的一般式方程与直线的垂直关系,直线的一般式方程与直线的平行关系
专题:直线与圆
分析:(I)由两条直线垂直的条件,建立关于m的方程,解之可得实数m的值
(II)根据两条直线平行的条件,建立关于m的关系式,即可得到使l1∥l2的实数m的值.
(II)根据两条直线平行的条件,建立关于m的关系式,即可得到使l1∥l2的实数m的值.
解答:
解(1)由 2m+(m+1)×1=0⇒3m+1=0⇒m=-
…(4分)
(2)由已知⇒2-(m+1)m=0⇒m2+m-2=0⇒m=-2或m=1…(6分)
当m=-2时⇒
满足 …(8分)
当m=1时⇒
不满足 …(10分)
综上m=-2 …(12分)
| 1 |
| 3 |
(2)由已知⇒2-(m+1)m=0⇒m2+m-2=0⇒m=-2或m=1…(6分)
当m=-2时⇒
|
当m=1时⇒
|
综上m=-2 …(12分)
点评:本题给出含有参数的两条直线方程,在两条直线平行或垂直的情况下,求参数m之值.着重考查了平面直角坐标系中两条直线平行、垂直的关系及其列式的知识,属于基础题.

练习册系列答案
相关题目
如果椭圆
+y2=k上两点间的距离最大值为8,则k的值为( )
| x2 |
| 4 |
| A、32 | B、16 | C、8 | D、4 |
已知a>0,a≠1,f(x)=x2-ax.当x∈(-1,1)时,均有f(x)<
,则实数a的取值范围是( )
| 1 |
| 2 |
A、(0,
| ||
B、[
| ||
C、(0,
| ||
D、[
|
若实数x,y满足条件
,则2x+y的最大值是( )
|
| A、8 | B、2 | C、4 | D、7 |
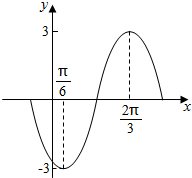 三角函数式:
三角函数式:
 如图所示,曲线是幂函数y=xa在第一象限内的图象,已知α分别取-1,1,
如图所示,曲线是幂函数y=xa在第一象限内的图象,已知α分别取-1,1,