题目内容
19．如图，在平行四边形OABC中，过点C（1，3）做CD⊥AB，垂足为点D，试求CD所在直线的一般式方程．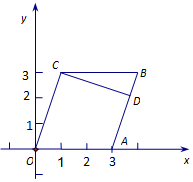
分析 根据原点坐标和已知的C点坐标，求出直线OC的斜率；根据平行四边形的两条对边平行得到AB平行于OC，又CD垂直与AB，所以CD垂直与OC，由（1）求出的直线OC的斜率，根据两直线垂直时斜率乘积为-1，求出CD所在直线的斜率，然后根据求出的斜率和点C的坐标写出直线CD的方程即可．
解答 解：因为点O（0，0），点C（1，3），
所以OC所在直线的斜率为${k_{OC}}=\frac{3-0}{1-0}=3$．（2分），
在平行四边形OABC中，AB∥OC，因为CD⊥AB，所以CD⊥OC．
所以 CD所在直线的斜率为${k_{CD}}=-\frac{1}{3}$．（6分）
所以CD所在直线方程为$y-3=-\frac{1}{3}（x-1）$，即x+3y-10=0．（10分）
点评 此题考查学生会根据两点的坐标求出过两点直线方程的斜率，掌握两直线平行时斜率所满足的条件，会根据一点和斜率写出直线的点斜式方程，是一道综合题．
练习册系列答案
相关题目
7．某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x（单位：千元）对年销售量y（单位：t）和年利润z（单位：千元）的影响，对近8年的年宣传费xi和年销售量yi（i=1，2，…，8）数据作了初步处理，得到下面的散点图及一些统计量的值．
表中wi=$\sqrt{x_i}$，$\overline w=\frac{1}{8}\sum_{i=1}^8{w_i}$
（1）若根据散点图用y=c+d$\sqrt{x}$表示年销售量y关于年宣传费x的回归方程，试根据表中数据，求c，d的值；
（2）已知这种产品的年利率z与x、y的关系为z=0.2y-x，根据（1）的结果回答下列问题：（i）年宣传费x=49时，年销售量及年利润的预报值是多少？
（ii）年宣传费x为何值时，年利润的预报值最大？
附：对于一组数据（u1，v1），（u2，v2），…，（un，vn），其回归直线v=α+βu的斜率和截距的最小二乘估计分别为：β=$\frac{{\sum_{i=1}^n{（{v_i}-\overline v）（{u_i}-\overline u）}}}{{\sum_{i=1}^n{{{（{u_i}-\overline u）}^2}}}}$α=$\overline v-β\overline u$．
| $\overline x$ | $\overline y$ | $\overline w$ | ${\sum_{i=1}^8{（{x_i}-\overline x）}^2}$ | ${\sum_{i=1}^8{（{w_i}-\overline w）}^2}$ | $\sum_{i=1}^8{（{x_i}-\overline x）}（{y_i}-\overline y）$ | $\sum_{i=1}^8{（{w_i}-\overline w）}（{y_i}-\overline y）$ |
| 46.6 | 56.3 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
（1）若根据散点图用y=c+d$\sqrt{x}$表示年销售量y关于年宣传费x的回归方程，试根据表中数据，求c，d的值；
（2）已知这种产品的年利率z与x、y的关系为z=0.2y-x，根据（1）的结果回答下列问题：（i）年宣传费x=49时，年销售量及年利润的预报值是多少？
（ii）年宣传费x为何值时，年利润的预报值最大？
附：对于一组数据（u1，v1），（u2，v2），…，（un，vn），其回归直线v=α+βu的斜率和截距的最小二乘估计分别为：β=$\frac{{\sum_{i=1}^n{（{v_i}-\overline v）（{u_i}-\overline u）}}}{{\sum_{i=1}^n{{{（{u_i}-\overline u）}^2}}}}$α=$\overline v-β\overline u$．
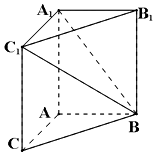如图，在三棱柱ABC-A1B1C1中，AA1C1C是边长为的正方形，平面ABC⊥平面AA1C1C，AB=3，BC=5．