Question

9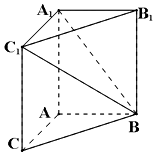．如图，在三棱柱ABC-A₁B₁C₁中，AA₁C₁C是边长为的正方形，平面ABC⊥平面AA₁C₁C，AB=3，BC=5．
（1）求证：AA₁⊥平面ABC；
（2）求二面角A₁-BC₁-B₁的余弦值；
（3）在线段BC₁上是否存在点D，使得AD⊥A₁B？若存在，求出$\frac{BD}{B{C}_{1}}$的值，若不存在，说明理由．

Answer 1

分析 （1）证明AA₁⊥AC．利用平面ABC⊥平面AA₁C₁C，且AA₁垂直于这两个平面的交线AC，推出结果．
（2）以A为原点建立空间直角坐标系A-xyz，求出相关点的坐标，求出平面A₁BC₁的法向量，平面BB₁C₁的法向量，利用向量的数量积求解二面角A₁-BC₁-B₁的余弦值．
（3）设D（x，y，z）是直线BC₁上一点，且$\overrightarrow{BD}$=$λ\overrightarrow{B{C}_{1}}$．求出$\overrightarrow{AD}$=（4λ，3-3λ，4λ）．通过$\overrightarrow{AD}$$•\overrightarrow{{A}_{1}B}=0$，求出$λ=\frac{9}{25}$．推出结果．

解答 解：（1）因为AA₁C₁C为正方形，所以AA₁⊥AC．
因为平面ABC⊥平面AA₁C₁C，且AA₁垂直于这两个平面的交线AC，
所以AA₁⊥平面ABC．…．（4分）
（2）由（I）知AA₁⊥AC，AA₁⊥AB．由题知AB=3，BC=5，AC=4，
所以AB⊥AC．
如图，以A为原点建立空间直角坐标系A-xyz，则B（0，3，0），
A₁（0，0，4），B₁（0，3，4），C₁（4，0，4），$\overrightarrow{{A}_{1}B}$=（0，3，-4），
$\overrightarrow{{A}_{1}{C}_{1}}$=（4，0，0）
设平面A₁BC₁的法向量为$\overrightarrow{n}$=（x，y，z），则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{{A}_{1}B}=0}\\{\overrightarrow{n}•\overrightarrow{{A}_{1}{C}_{1}}=0}\end{array}\right.$，即$\left\{\begin{array}{l}{3y-4z=0}\\{4x=0}\end{array}\right.$，
令z=3，则x=0，y=4，所以$\overrightarrow{n}$=（0，4，3）．
同理可得，平面BB₁C₁的法向量为$\overrightarrow{m}$=（3，4，0），所以cos$＜\overrightarrow{n}，\overrightarrow{m}＞$=$\frac{\overrightarrow{n}•\overrightarrow{m}}{|\overrightarrow{n}||\overrightarrow{m}|}$=$\frac{16}{25}$．
由题知二面角A₁-BC₁-B₁为锐角，所以二面角A₁-BC₁-B₁的余弦值为$\frac{16}{25}$．…（8分）
（3）设D（x，y，z）是直线BC₁上一点，且$\overrightarrow{BD}$=$λ\overrightarrow{B{C}_{1}}$．
所以（x，y-3，z）=λ（4，-3，4）．解得x=4λ，y=3-3λ，z=4λ．
所以$\overrightarrow{AD}$=（4λ，3-3λ，4λ）．
由$\overrightarrow{AD}$$•\overrightarrow{{A}_{1}B}=0$，即9-25λ=0．解得$λ=\frac{9}{25}$．
因为$\frac{9}{25}$∈（0，1），所以在线段BC₁上存在点D，使得AD⊥A₁B．
此时，$\frac{BD}{B{C}_{1}}$=λ=$\frac{9}{25}$．…（12分）

点评 本题考查二面角的平面角的求法，平面与平面垂直的性质定理的应用，考查空间想象能力以及逻辑推理能力．