题目内容
已知函数f(x)=lnx+
-1(a>-1).
(Ⅰ)当a=0,求f(x)的单调区间;
(Ⅱ)当x∈[e,+∞)时,有x•f(x)≥2a恒成立(e=2.71828…),求a的取值范围.
| a+1 |
| x |
(Ⅰ)当a=0,求f(x)的单调区间;
(Ⅱ)当x∈[e,+∞)时,有x•f(x)≥2a恒成立(e=2.71828…),求a的取值范围.
考点:函数的单调性及单调区间,函数单调性的判断与证明,函数恒成立问题
专题:计算题,函数的性质及应用,导数的综合应用,不等式的解法及应用
分析:(Ⅰ)求出a=0的f(x)的解析式,注意x>0,求出导数,令导数大于0,得增区间,令导数小于0,得减区间;
(Ⅱ)当x∈[e,+∞)时,有x•f(x)≥2a恒成立,即a≤xlnx-x+1在[e,+∞)恒成立.构造函数g(x)=xlnx-x+1,运用导数判断g(x)的单调性,求出最小值,即可得到a的范围.
(Ⅱ)当x∈[e,+∞)时,有x•f(x)≥2a恒成立,即a≤xlnx-x+1在[e,+∞)恒成立.构造函数g(x)=xlnx-x+1,运用导数判断g(x)的单调性,求出最小值,即可得到a的范围.
解答:
解:(Ⅰ)当a=0,f(x)=lnx+
-1(x>0),
f′(x)=
-
=
,
当x>1时,f′(x)>0,则f(x)在(1,+∞)上递增;
当0<x<1时,f′(x)<0,则f(x)在(0,1)上递减.
综上可得f(x)的增区间为(1,+∞),减区间为(0,1).
(Ⅱ)当x∈[e,+∞)时,有x•f(x)≥2a恒成立,
即为2a≤x(lnx+
-1)=xlnx-x+a+1,
即a≤xlnx-x+1在[e,+∞)恒成立.
令g(x)=xlnx-x+1,
g′(x)=lnx+x•
-1=lnx,
当x∈[e,+∞)时,g′(x)≥1>0,
即g(x)在[e,+∞)递增,
则g(x)的最小值为g(e)=elne-e+1=1.
即有a≤1.
| 1 |
| x |
f′(x)=
| 1 |
| x |
| 1 |
| x2 |
| x-1 |
| x2 |
当x>1时,f′(x)>0,则f(x)在(1,+∞)上递增;
当0<x<1时,f′(x)<0,则f(x)在(0,1)上递减.
综上可得f(x)的增区间为(1,+∞),减区间为(0,1).
(Ⅱ)当x∈[e,+∞)时,有x•f(x)≥2a恒成立,
即为2a≤x(lnx+
| a+1 |
| x |
即a≤xlnx-x+1在[e,+∞)恒成立.
令g(x)=xlnx-x+1,
g′(x)=lnx+x•
| 1 |
| x |
当x∈[e,+∞)时,g′(x)≥1>0,
即g(x)在[e,+∞)递增,
则g(x)的最小值为g(e)=elne-e+1=1.
即有a≤1.
点评:本题主要考查导数的运用:求单调区间、求极值和最值,考查不等式的恒成立问题转化为求函数的最值问题,考查运算能力,属于中档题.

练习册系列答案
相关题目
双曲线
-
=1(a>0,b>0)的离心率为2,则它的一条渐近线经过点( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、(1,2) | ||
| B、(2,1) | ||
C、(1,
| ||
D、(
|
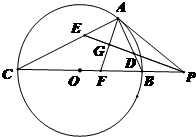 如图:已知PA与圆O相切于点A,经过点O的割线PBC交圆O于点B,C,∠APC的平分线分别交AB,AC于点D,E,.点G是线段ED的中点,AG的延长线与CP相交于点F.
如图:已知PA与圆O相切于点A,经过点O的割线PBC交圆O于点B,C,∠APC的平分线分别交AB,AC于点D,E,.点G是线段ED的中点,AG的延长线与CP相交于点F.