题目内容
已知焦点在x轴的双曲线上一点P到双曲线两个焦点的距离分别为4和8,直线y=x-2被双曲线截得的弦长为20
,求双曲线的标准方程.
| 2 |
考点:双曲线的标准方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:利用双曲线上一点P到双曲线两个焦点的距离分别为4和8,求出a,直线y=x-2代入
-
=1可得(b2-4)x2+16x-16-4b2=0,利用直线y=x-2被双曲线截得的弦长为20
,求出b,即可求双曲线的标准方程.
| x2 |
| 4 |
| y2 |
| b2 |
| 2 |
解答:
解:设双曲线方程为
-
=1(a>0,b>0),则
∵双曲线上一点P到双曲线两个焦点的距离分别为4和8,
∴2a=8-4,
∴a=2,
∴双曲线方程为
-
=1,
直线y=x-2代入
-
=1可得(b2-4)x2+16x-16-4b2=0,
设交点为(x1,y1),(x2,y2),则x1+x2=-
,x1x2=
,
∴(20
)2=(1+1)•[(-
)2-4×
],
∴b2=20,
∴双曲线方程为
-
=1.
| x2 |
| a2 |
| y2 |
| b2 |
∵双曲线上一点P到双曲线两个焦点的距离分别为4和8,
∴2a=8-4,
∴a=2,
∴双曲线方程为
| x2 |
| 4 |
| y2 |
| b2 |
直线y=x-2代入
| x2 |
| 4 |
| y2 |
| b2 |
设交点为(x1,y1),(x2,y2),则x1+x2=-
| 16 |
| b2-4 |
| -16-4b2 |
| b2-4 |
∴(20
| 2 |
| 16 |
| b2-4 |
| -16-4b2 |
| b2-4 |
∴b2=20,
∴双曲线方程为
| x2 |
| 4 |
| y2 |
| 20 |
点评:本题考查求双曲线的标准方程,考查直线与双曲线的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
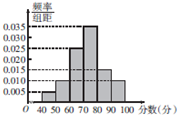 某校学生在一次学业水平测试中的数学成绩制成如图所示的频率分布直方图,60分以下的人要补考,已知90分以上的有80人,则该校需要补考的人数为( )
某校学生在一次学业水平测试中的数学成绩制成如图所示的频率分布直方图,60分以下的人要补考,已知90分以上的有80人,则该校需要补考的人数为( )| A、120 | B、150 |
| C、180 | D、200 |
设a2-a>0,函数y=a|x|(a>0,a≠1)的图象形状大致是( )
A、 |
B、 |
C、 |
D、 |