题目内容
设α∈(0,
),函数f(x)的定义域为[0,1],且f(0)=0,f(1)=1,当x≥y时,有f(
)=f(x)sinα+(1-sinα)f(y)
(1)求f(
),f(
);
(2)求α的值
(3)求函数g(x)=sin(α-2x)的单调增区间.
| π |
| 2 |
| x+y |
| 2 |
(1)求f(
| 1 |
| 2 |
| 1 |
| 4 |
(2)求α的值
(3)求函数g(x)=sin(α-2x)的单调增区间.
考点:正弦函数的单调性,函数的值
专题:三角函数的图像与性质
分析:(1)利用赋值法即可求f(
),f(
);
(2)建立方程关系,利用三角函数的关系即可求α的值
(3)根据三角函数的单调性,建立不等式关系即可求函数g(x)=sin(α-2x)的单调增区间.
| 1 |
| 2 |
| 1 |
| 4 |
(2)建立方程关系,利用三角函数的关系即可求α的值
(3)根据三角函数的单调性,建立不等式关系即可求函数g(x)=sin(α-2x)的单调增区间.
解答:
解:(1)当x=0,y=1时,由f(
)=f(x)sinα+(1-sinα)f(y)
得f(
)=f(
)sinα+(1-sinα)f(0)=sinα,
f(
)=f(
)=f(
)sinα+(1-sinα)f(0)=sin2α,
(2)f(
)=f(
)=f(1)sinα+(1-sinα)f(
)=sinα(2-sinα),
即f(
)=f(
)=f(
)sinα+(1-sinα)f(
)=sin2α(3-2sinα),
∴sinα=sin2α(3-2sinα),
∴sinα=0或1或
.
∵α∈(0,
),∴α=
.
(3)g(x)=sin(α-2x)=sin(
-2x)=sin(2x+
),
由-
+2kπ≤2x+
≤
+2kπ,
解得kπ-
≤x≤kπ-
,
∴g(x)的单调增区间为[kπ-
,kπ-
]k∈Z.
| x+y |
| 2 |
得f(
| 1 |
| 2 |
| 1 |
| 2 |
f(
| 1 |
| 4 |
| ||
| 2 |
| 1 |
| 2 |
(2)f(
| 3 |
| 4 |
1+
| ||
| 2 |
| 1 |
| 2 |
即f(
| 1 |
| 2 |
| ||||
| 2 |
| 3 |
| 4 |
| 1 |
| 4 |
∴sinα=sin2α(3-2sinα),
∴sinα=0或1或
| 1 |
| 2 |
∵α∈(0,
| π |
| 2 |
| π |
| 6 |
(3)g(x)=sin(α-2x)=sin(
| π |
| 6 |
| 5π |
| 6 |
由-
| π |
| 2 |
| 5π |
| 6 |
| π |
| 2 |
解得kπ-
| 2π |
| 3 |
| π |
| 6 |
∴g(x)的单调增区间为[kπ-
| 2π |
| 3 |
| π |
| 6 |
点评:本题主要考查三角函数的单调性的判断,利用抽象函数,利用赋值法是解决本题的关键.

练习册系列答案
相关题目
已知角θ=30°,则sinθ的值是( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
下列函数中,在(0,+∞)上是减函数的是( )
A、y=
| |||||
| B、y=x2 | |||||
| C、y=2x | |||||
D、y=
|
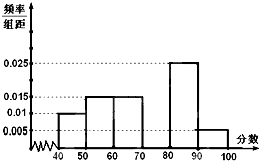 某校从参加高一年级期中考试的学生中抽出60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60)…,[80,90),[90,100],然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高一年级期中考试的学生中抽出60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60)…,[80,90),[90,100],然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题: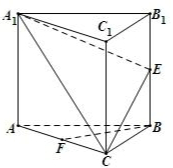 如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.
如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.