题目内容
已知角α的终边经过点P（-3，-
）．
（Ⅰ）求sinα、cosα、tanα的值；
（Ⅱ）求
-
的值．
| 3 |
（Ⅰ）求sinα、cosα、tanα的值；
（Ⅱ）求
|
|
考点：任意角的三角函数的定义,三角函数的化简求值
专题：三角函数的求值
分析：（Ⅰ）直接利用三角函数的定义求sinα、cosα、tanα的值；
（Ⅱ）化简表达式
-
，代入（Ⅰ）的值求解即可．
（Ⅱ）化简表达式
|
|
解答：
解：（Ⅰ）由三角函数的定义得r=
=2
．
∴sinα=
=
=-
，cosα=
=
=-
，tanα=
=
=
．
（Ⅱ）
-
=
-
=
-
=-2tanα=-
．
(-3)2+(-
|
| 3 |
∴sinα=
| y |
| r |
-
| ||
2
|
| 1 |
| 2 |
| x |
| r |
| -3 | ||
2
|
| ||
| 2 |
| y |
| x |
-
| ||
| -3 |
| ||
| 3 |
（Ⅱ）
|
|
|
|
| 1+sinα |
| -cosα |
| 1-sinα |
| -cosα |
2
| ||
| 3 |
点评：本题考查三角函数的定义的应用，三角函数的化简求值，考查计算能力．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
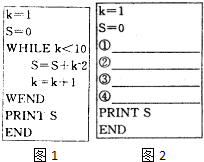图1给出一个用“当型”循环语句编写的程序：
在2014年清明节期间，高速公路车辆较多，某调查公司在服务区从七座以下小型汽车中，按进服务区的先后每间隔50辆就抽取一辆的抽样方法，抽取40名驾驶员进行调查，将他们在某段高速公路上的车速（km/h）分成6段：（60，65），[65，70），[70，75），[80，85），[85，90）后得到如图的频率分布直方图．