题目内容
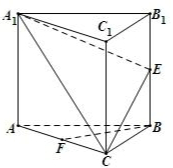 如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.
如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.(1)求证:BF∥平面A1EC;
(2)求证:平面A1EC⊥平面ACC1A1.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:(1)连接A1C与AC1交于点O,连接OF,证明四边形BEOF是平行四边形,可得BF∥OE,利用线面平行的判定定理,即可证明BF∥平面A1EC;
(2)证明平面A1EC⊥平面ACC1A1,只需证明OE⊥平面A1EC.
(2)证明平面A1EC⊥平面ACC1A1,只需证明OE⊥平面A1EC.
解答:
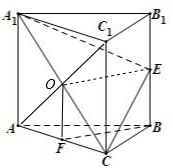 证明:(1)连接A1C与AC1交于点O,连接OF,
证明:(1)连接A1C与AC1交于点O,连接OF,
∵F为AC的中点,
∴OF∥C1C且OF=
C1C,
∵E为BB1的中点,
∴BE∥C1C且BE=
C1C,
∴BE∥OF且BE=OF,
∴四边形BEOF是平行四边形,
∴BF∥OE,
∵BF?平面A1EC,OE?平面A1EC,
∴BF∥平面A1EC
(2)∵AB=CB,F为AC的中点,
∴BF⊥AC
由(1)知BF∥OE,
∴OE⊥AC,
∵AA1⊥底面ABC,BF?底面ABC,
∴AA1⊥BF,
∵BF∥OE,
∴OE⊥AA1,
∵AA1∩AC=A,
∴OE⊥平面AA1C1C
∵OE?面A1EC,
∴平面A1EC⊥平面AA1C1C.
 证明:(1)连接A1C与AC1交于点O,连接OF,
证明:(1)连接A1C与AC1交于点O,连接OF,∵F为AC的中点,
∴OF∥C1C且OF=
| 1 |
| 2 |
∵E为BB1的中点,
∴BE∥C1C且BE=
| 1 |
| 2 |
∴BE∥OF且BE=OF,
∴四边形BEOF是平行四边形,
∴BF∥OE,
∵BF?平面A1EC,OE?平面A1EC,
∴BF∥平面A1EC
(2)∵AB=CB,F为AC的中点,
∴BF⊥AC
由(1)知BF∥OE,
∴OE⊥AC,
∵AA1⊥底面ABC,BF?底面ABC,
∴AA1⊥BF,
∵BF∥OE,
∴OE⊥AA1,
∵AA1∩AC=A,
∴OE⊥平面AA1C1C
∵OE?面A1EC,
∴平面A1EC⊥平面AA1C1C.
点评:本小题主要考查线面平行,平面与平面垂直的判定等有关基础知识,考查空间想象能力、运算能力和推理论证能力,考查转化思想,属于中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
已知a=log1.20.3,b=log1.20.8,c=1.50.5,则a,b,c的大小关系为( )
| A、a>b>c |
| B、c>a>b |
| C、a>c>b |
| D、c>b>a |
“-3<m<-1”是方程
+
=1表示双曲线的( )
| x2 |
| 2+m |
| y2 |
| m+1 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
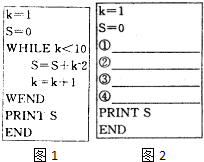 图1给出一个用“当型”循环语句编写的程序:
图1给出一个用“当型”循环语句编写的程序: