题目内容
已知函数f(x)=lnx-
(Ⅰ)若函数f(x)在(0,+∞)上为单调递增函数,求实数a的取值范围;
(Ⅱ)设m>n>0,求证:
>
.
| a(x-1) |
| x+1 |
(Ⅰ)若函数f(x)在(0,+∞)上为单调递增函数,求实数a的取值范围;
(Ⅱ)设m>n>0,求证:
| lnm-lnn |
| 2 |
| m-n |
| m+n |
考点:利用导数研究函数的单调性,函数单调性的性质
专题:导数的综合应用
分析:(Ⅰ)f′(x)=
,根据题意,在(0,+∞)上恒有f′(x)≥0,即x2+2(1-a)x+1≥0,解不等式求出即可;
(Ⅱ)原式?ln
-
>0,由
>1 得f(
)>f(1),而f(1)=0,从而问题得证.
| x2+2(1-a)x+1 |
| x(x+1)2 |
(Ⅱ)原式?ln
| m |
| n |
2(
| ||
|
| m |
| n |
| m |
| n |
解答:
解:(Ⅰ)∵f′(x)=
,
根据题意,在(0,+∞)上恒有f′(x)≥0,
即x2+2(1-a)x+1≥0,
∴a≤
(x+
)+1,
∵x+
≥2,
∴y=
(x+
)+1≥2,
∴a≤2,
a的取值范围是(-∞,2];
(Ⅱ)原式?ln
-
>0,
由(Ⅰ)得a=2时f(x)在(0,+∞)上为增函数
∵m>n>0,
∴
>1,
∴f(
)>f(1),
而f(1)=0,
∴原式成立.
| x2+2(1-a)x+1 |
| x(x+1)2 |
根据题意,在(0,+∞)上恒有f′(x)≥0,
即x2+2(1-a)x+1≥0,
∴a≤
| 1 |
| 2 |
| 1 |
| x |
∵x+
| 1 |
| x |
∴y=
| 1 |
| 2 |
| 1 |
| x |
∴a≤2,
a的取值范围是(-∞,2];
(Ⅱ)原式?ln
| m |
| n |
2(
| ||
|
由(Ⅰ)得a=2时f(x)在(0,+∞)上为增函数
∵m>n>0,
∴
| m |
| n |
∴f(
| m |
| n |
而f(1)=0,
∴原式成立.
点评:本题考察了函数的单调性,导数的应用,分离参数法,不等式的证明,是一道中档题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
已知数列{an}满足的前n项和Sn=n2+n+1,那么它的通项公式为an=( )
| A、an=n+1 | |||||
B、an=
| |||||
| C、an=2n | |||||
D、an=
|
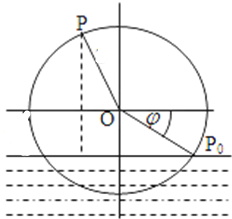 一半径为2
一半径为2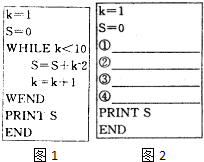 图1给出一个用“当型”循环语句编写的程序:
图1给出一个用“当型”循环语句编写的程序: