Question

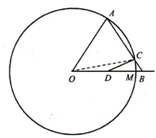如图，半径为1的圆O上有一定点M，A为圆O上的动点．在射线OM上有一动点B，AB=1，0B＞1．线段AB交圆O于另一点C，D为线段的OB中点．求线段CD长的取值范围．

Answer 1

考点：余弦定理

专题：解三角形

分析：设∠AOB=θ，由OA=AB=1，利用等边对等角及内角和定理表示出∠OBA与∠BAO，再由OA=OC，表示出∠OCA与∠BOC，连接AD，根据OA=AB，D为OB中点，利用三线合一得到A垂直于OB，表示出OD，在三角形OCD中，利用余弦定理表示出CD，根据同角三角函数间的基本关系及二次函数性质求出范围即可．

解答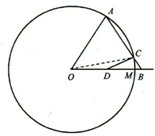： 解：连接AD，
设∠AOB=θ，
∵OA=AB=1，
∴∠OBA=θ，∠BAO=180°-2θ，
∵OA=OC，
∴∠OCA=180°-2θ，
∴∠BOC=180°-3θ，
∵OA=AB，D为OB中点，
∴AD⊥OB，
∴OD=OAcosθ=cosθ，
在△OCD中，利用余弦定理得：CD²=OC²+OD²-2OC•OD•cos∠BOC
=1+cos²θ-2cosθcos（180°-θ）
=1+cos²θ+2cosθcos3θ=8cos⁴θ-5cos²θ+1
=8（cos²θ-

5

16

）²+

7

32

，
∵∠BOC=180°-3θ＜∠AOB=θ，∠OCA=180°-2θ＞∠OBA=θ，
∴

180°-3θ＜θ 180°-2θ＞θ

，
解得：45°＜θ＜60°，即

1

4

＜cos²θ＜

1

2

，
∴

7

32

＜CD²＜

1

2

，
即

14

8

≤CD＜

2

2

，等号在cosθ=

5

4

时成立，
则线段CD长的取值范围是[

14

8

，

2

2

）．

点评：此题考查了余弦定理，二次函数性质，等腰三角形的性质，以及余弦函数的性质，熟练掌握余弦定理是解本题的关键．