题目内容
13.函数f(x)=Asin(ωx-φ)+m(A>0,ω>0,0<φ<$\frac{π}{2}$)的最大值为3,最小值为-1,其图象两条对称轴之间的最短距离为$\frac{π}{2}$,且f($\frac{π}{2}$)=1.(1)求函数f(x)的解析式;
(2)求函数g(x)=f(x+$\frac{π}{12}$)-f(x+$\frac{π}{4}$)的单调递减区间.
分析 (1)由函数的最值求出A和m,由周期求出ω,由f($\frac{π}{12}$)=1,结合φ∈(0,$\frac{π}{2}$),解得φ,可得函数的解析式.
(2)先求g(x),由2kπ+$\frac{π}{2}$≤2x-$\frac{π}{3}$≤2kπ+$\frac{3π}{2}$,k∈Z即可解得单调递减区间.
解答 (本题满分为12分)
解:(1)由题意可得:A+m=3,-A+m=-1,
解得:A=2,m=1.
∵图象两条对称轴之间的最短距离为$\frac{π}{2}$,
∴函数f(x)的最小正周期T=π,即$ω=\frac{2π}{π}=2$.
∵f($\frac{π}{12}$)=1,
∴sin($\frac{π}{6}$-φ)=0,又φ∈(0,$\frac{π}{2}$),
∴解得:φ=$\frac{π}{6}$.
故函数f(x)的解析式为:f(x)=2sin(2x-$\frac{π}{6}$)+1…6分
(2)g(x)=f(x+$\frac{π}{12}$)-f(x+$\frac{π}{4}$)=2sin2x=2sin(2x+$\frac{π}{3}$)=sin2x-$\sqrt{3}$2x=2sin(2x-$\frac{π}{3}$),…8分
由2kπ+$\frac{π}{2}$≤2x-$\frac{π}{3}$≤2kπ+$\frac{3π}{2}$,k∈Z即可解得单调递减区间为:[k$π+\frac{5π}{12}$,k$π+\frac{11π}{12}$],k∈Z.…12分
点评 本题主要考查由函数y=Asin(ωx+φ)+B的部分图象求解析式,由函数的最值求出A和B,由周期求出ω,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.一质点按规律S(t)=2t3+1运动,则t=1时的瞬时速度为( )
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
4.正三棱柱ABC-A1B1C1各棱长均为1,M为CC1的中点,则点B1到截面A1BM的距离为( )
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
18.已知函数$f(x)=a-\frac{4}{{{2^x}+1}}({a∈R})$是定义在(-∞,+∞)上的奇函数.
(1)求a的值,并写出函数f(x)的解析式;
(2)求证:函数f(x)在上是增函数.
(1)求a的值,并写出函数f(x)的解析式;
(2)求证:函数f(x)在上是增函数.
5.“抛物线y=ax2的准线方程为y=2”是“抛物线y=ax2的焦点与双曲线$\frac{y^2}{3}-{x^2}=1$的焦点重合”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
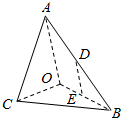 如图,在三棱锥AB0C中.AO⊥平面BOC,∠OAB=∠OAC=$\frac{π}{6}$.AB=AC=2.BC=$\sqrt{2}$,D,E分别为AB,OB的中点.
如图,在三棱锥AB0C中.AO⊥平面BOC,∠OAB=∠OAC=$\frac{π}{6}$.AB=AC=2.BC=$\sqrt{2}$,D,E分别为AB,OB的中点.